LUSBY TAYLOR'S METHOD
This elegant method, devised by Chris Lusby Taylor, uses the ancient Greek equant method in order to calculate the Sun's true longitude and thus the Eccentricity Effect. It then uses a geometrically correct method to find the Obliquity Effect.
Although the method very closely produces an elliptical path for the sun, it does not correctly emulate Kepler's 3rd Law that equal areas are swept out in equal times.
The errors produced are a few secs.
UPDATE - thanks to personal communication from Chris Lusby Taylor
Ptolemy puts the Equant Point and the Earth equal distances either side of the centre of the circular orbit of the sun. Chris can show that a far more accurate model, which almost precisely gives the Keplerian 3rd law of equal swept areas, results from putting the centre of the orbit - not mid-way between the Earth and Equant - but rather 3/8 of the way. Strange, but true! Documentation on this change will be forthcoming,
All that is wanted is a mechanical method to simulate the geometry. This would be useful since it produces its result on an arc of a Circle - easily translated to rotation of a dial plate. Other methods of mechanically simulating the EoT produce results in a linear fashion- requiring a rack and pinion or a chain system to convert to rotary motion.
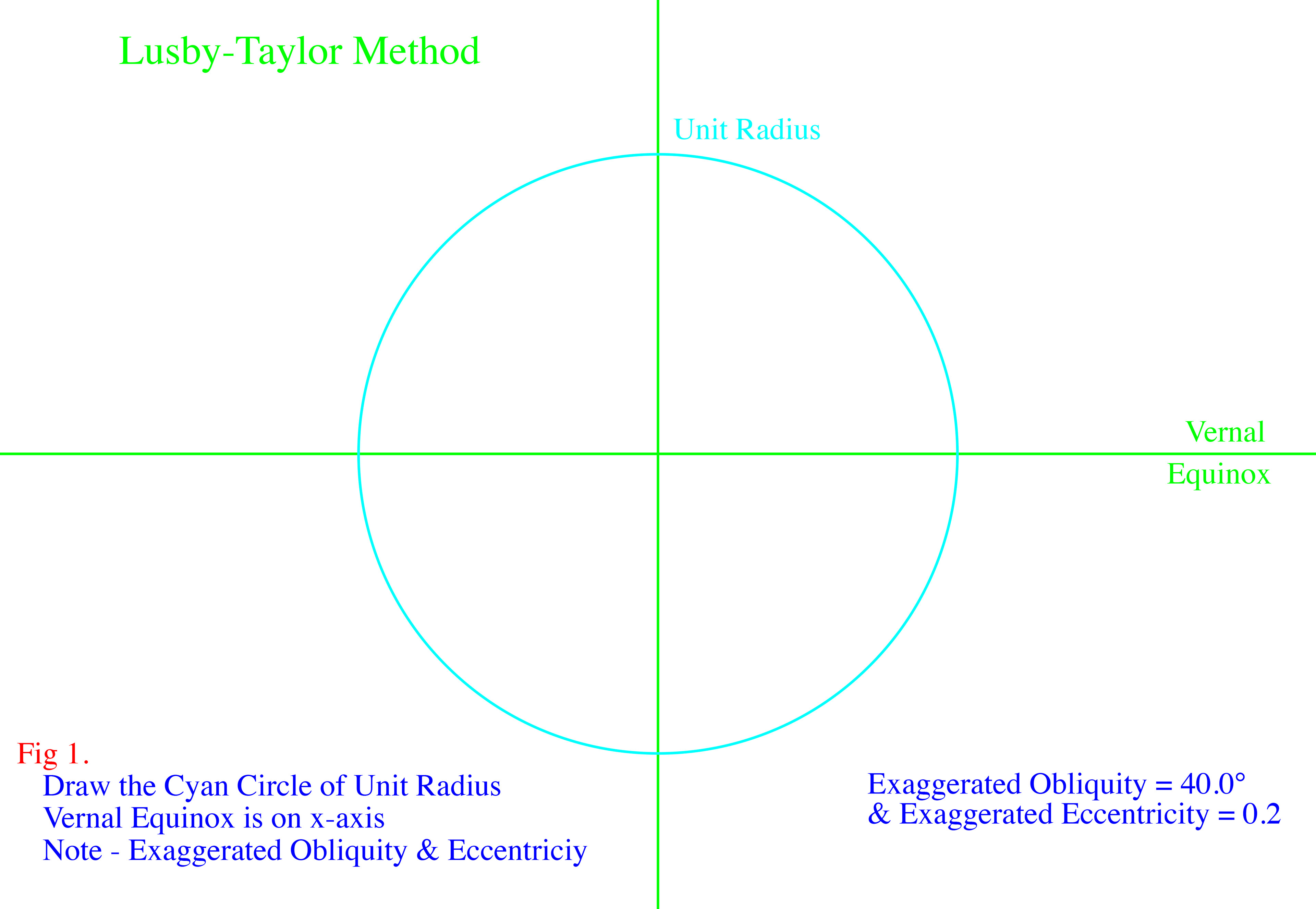
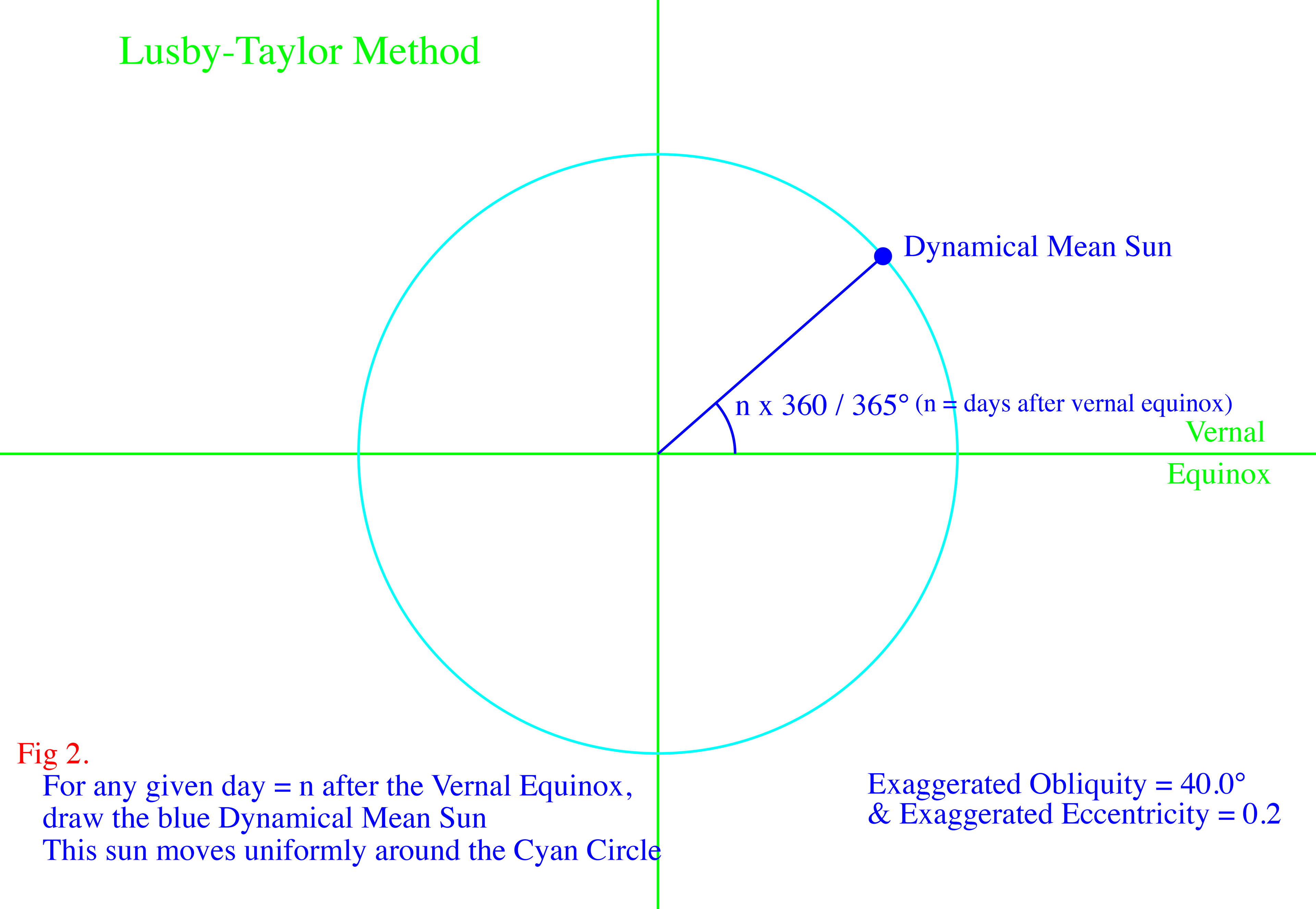
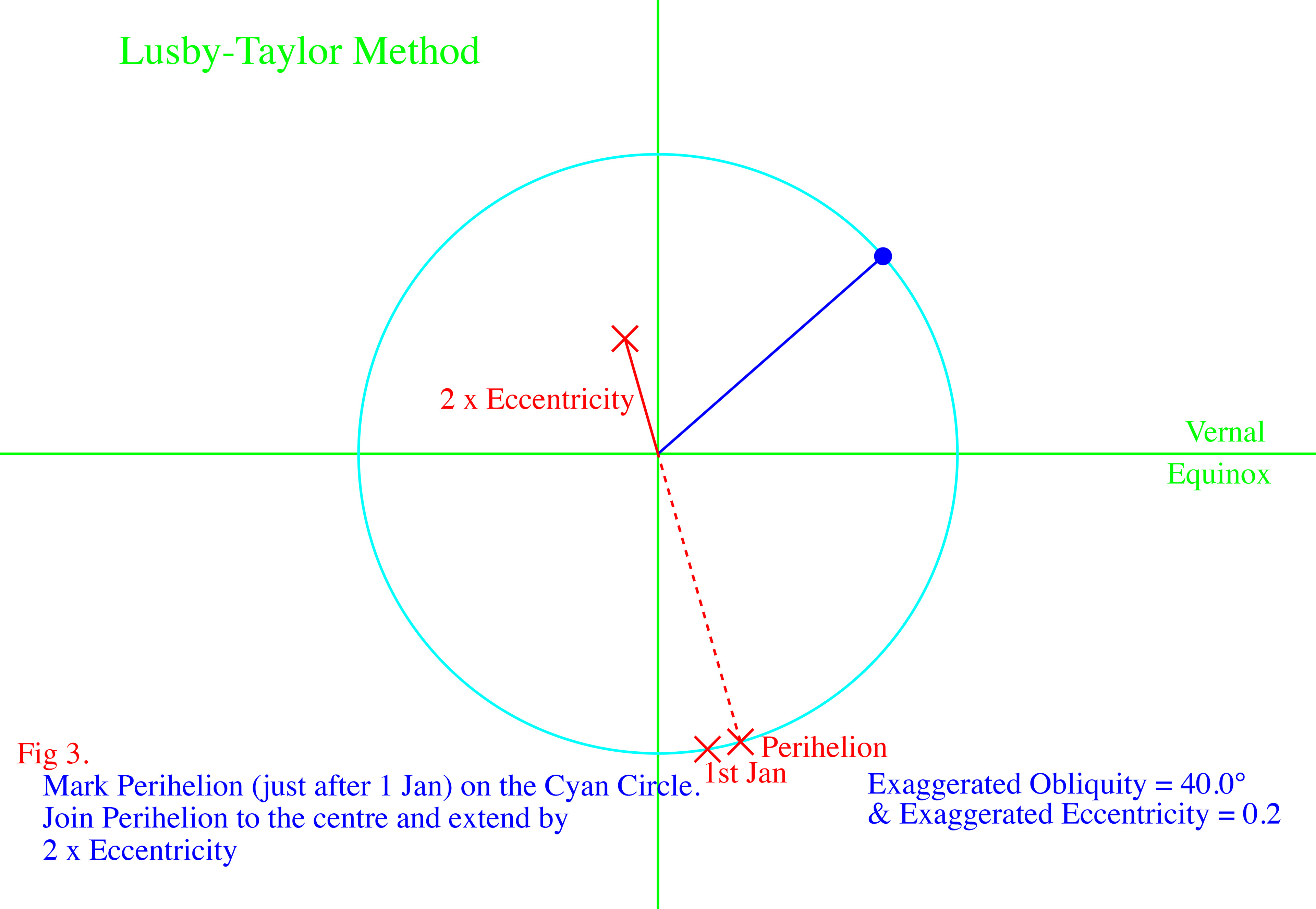
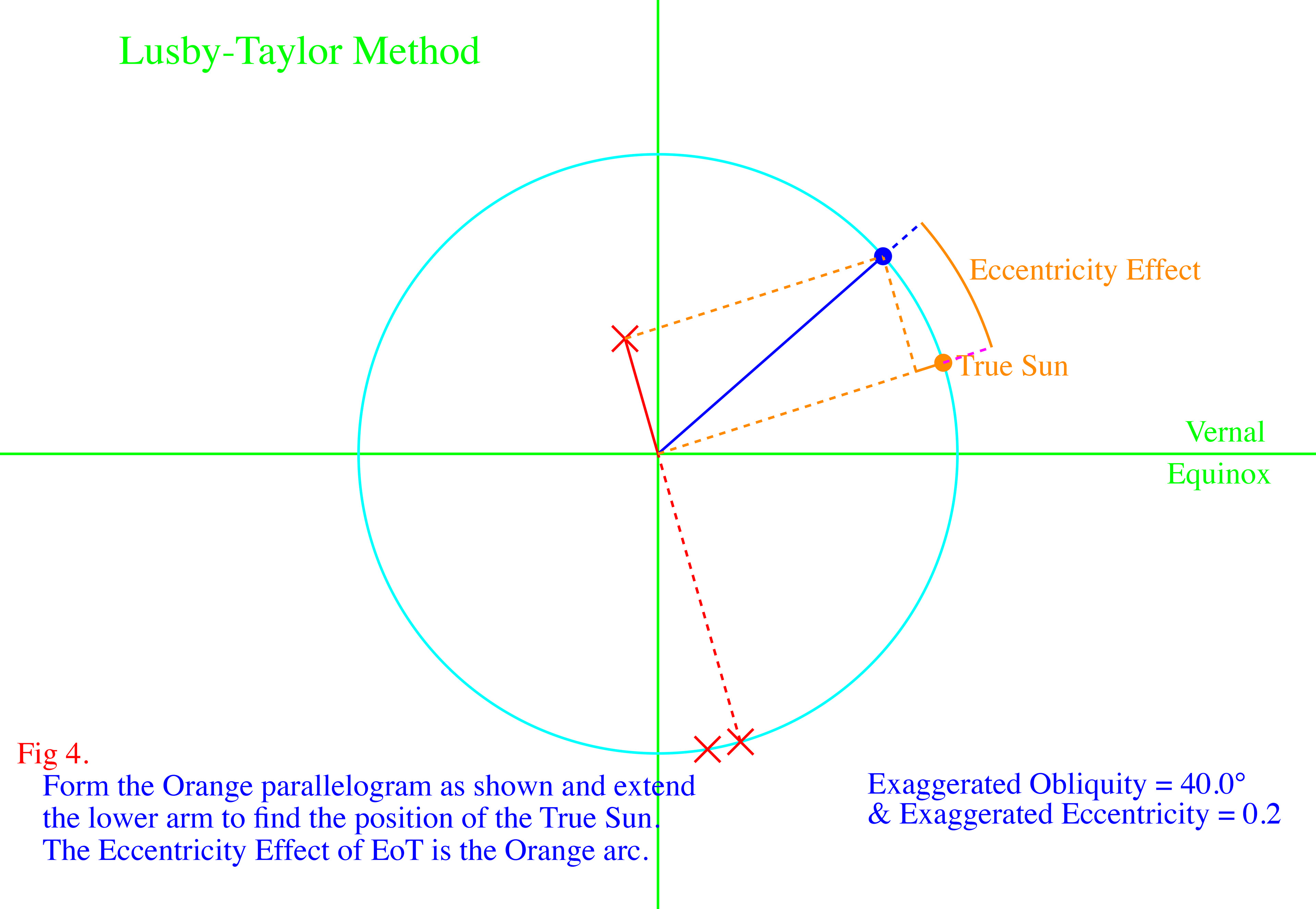
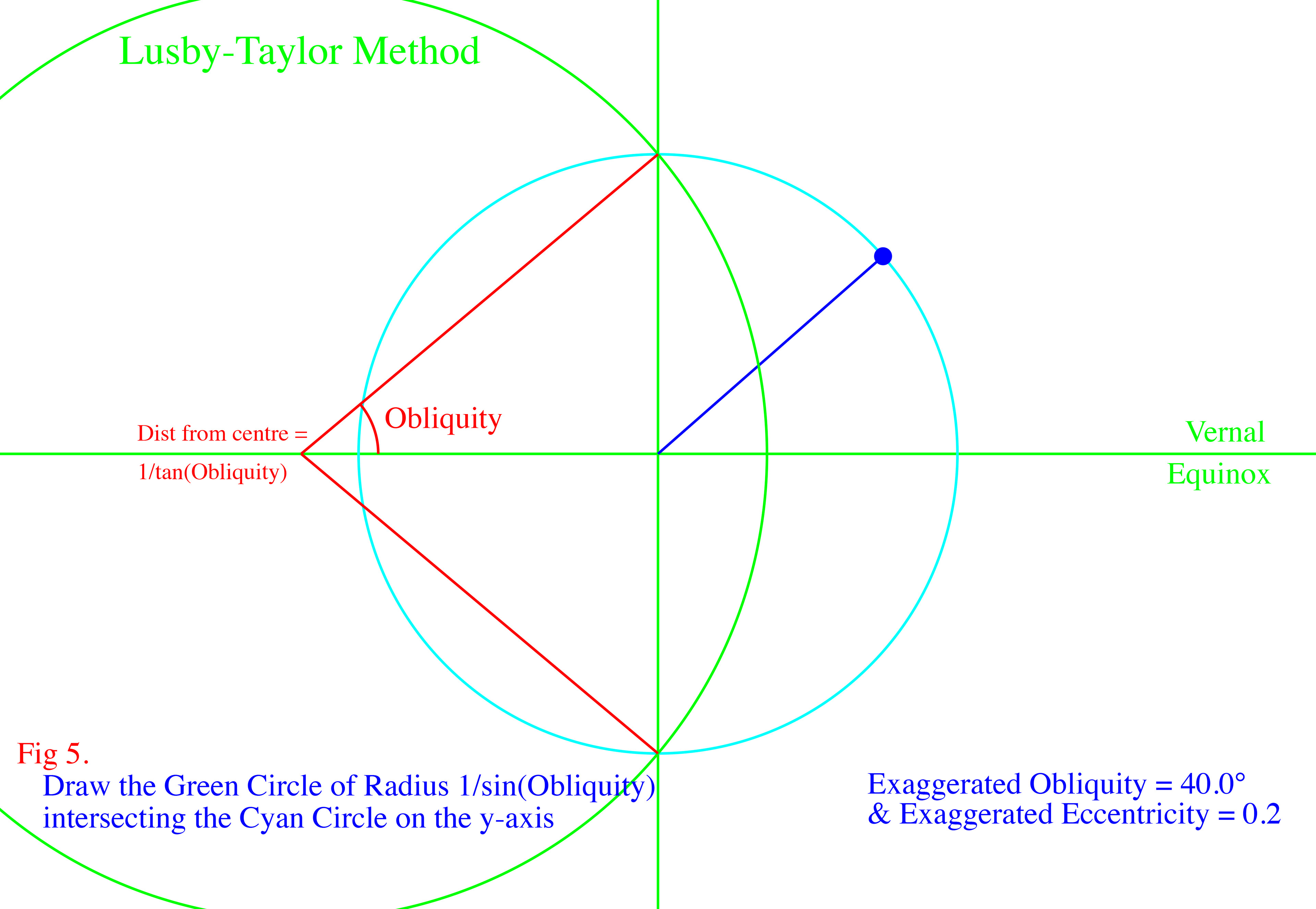
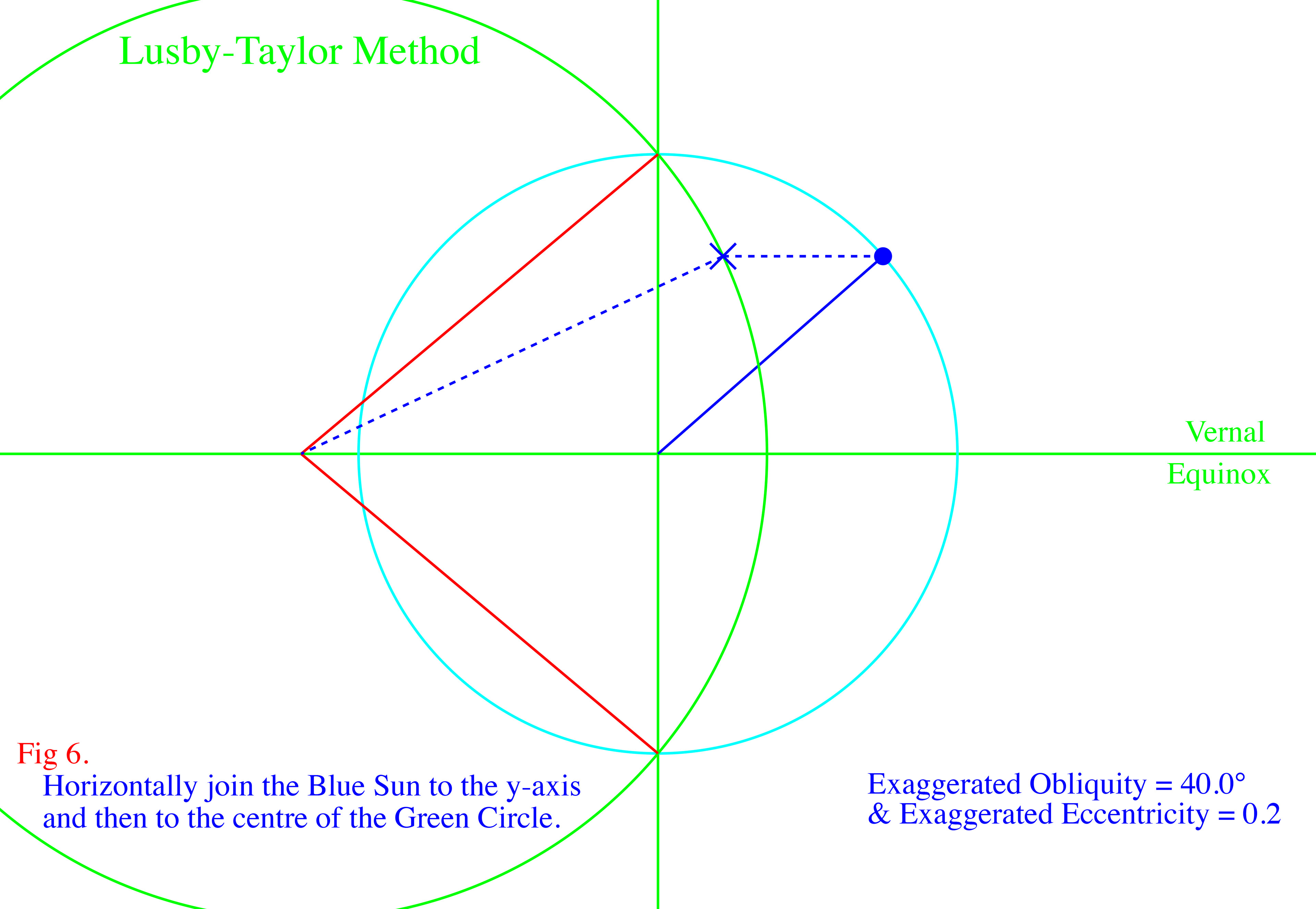
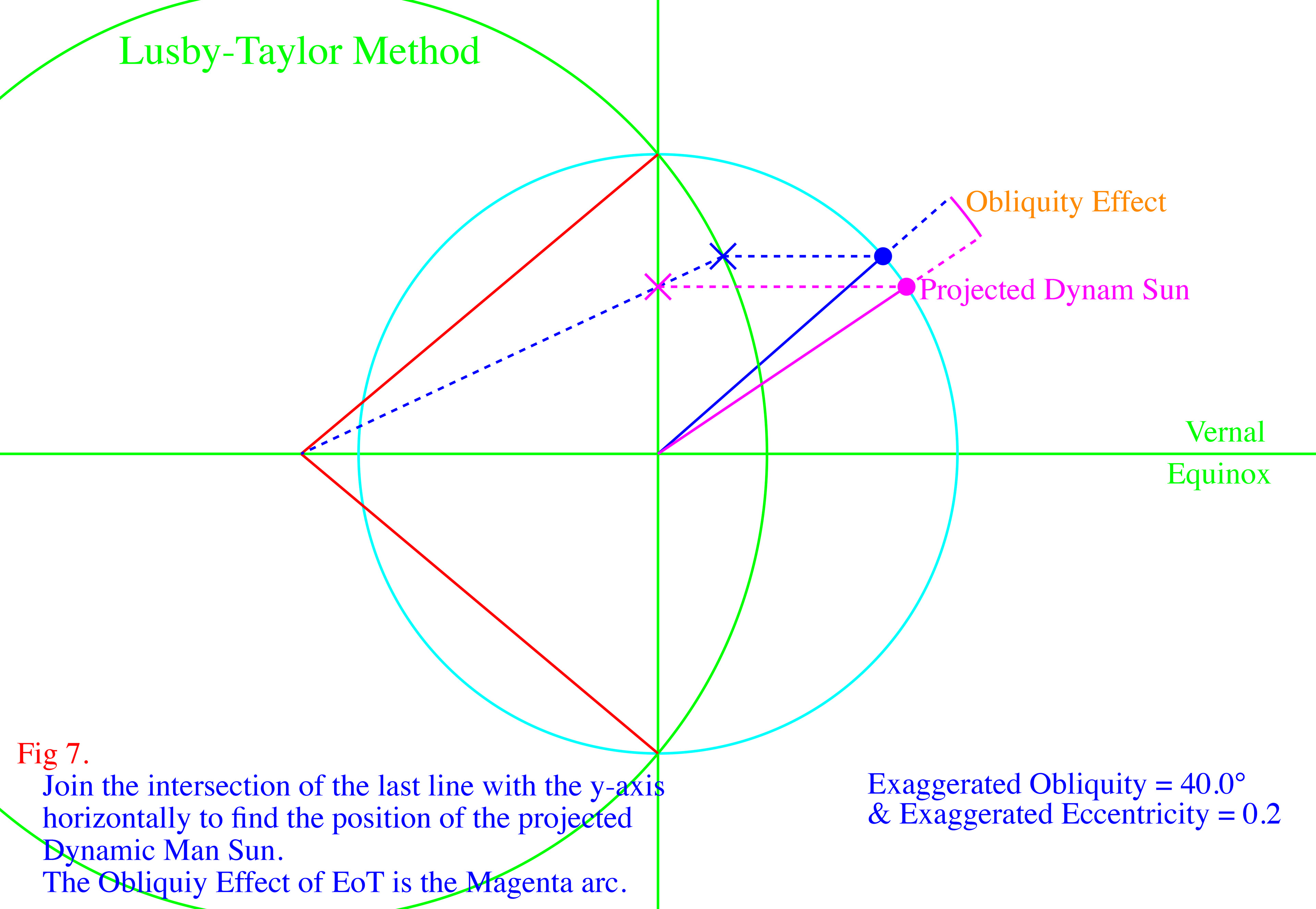
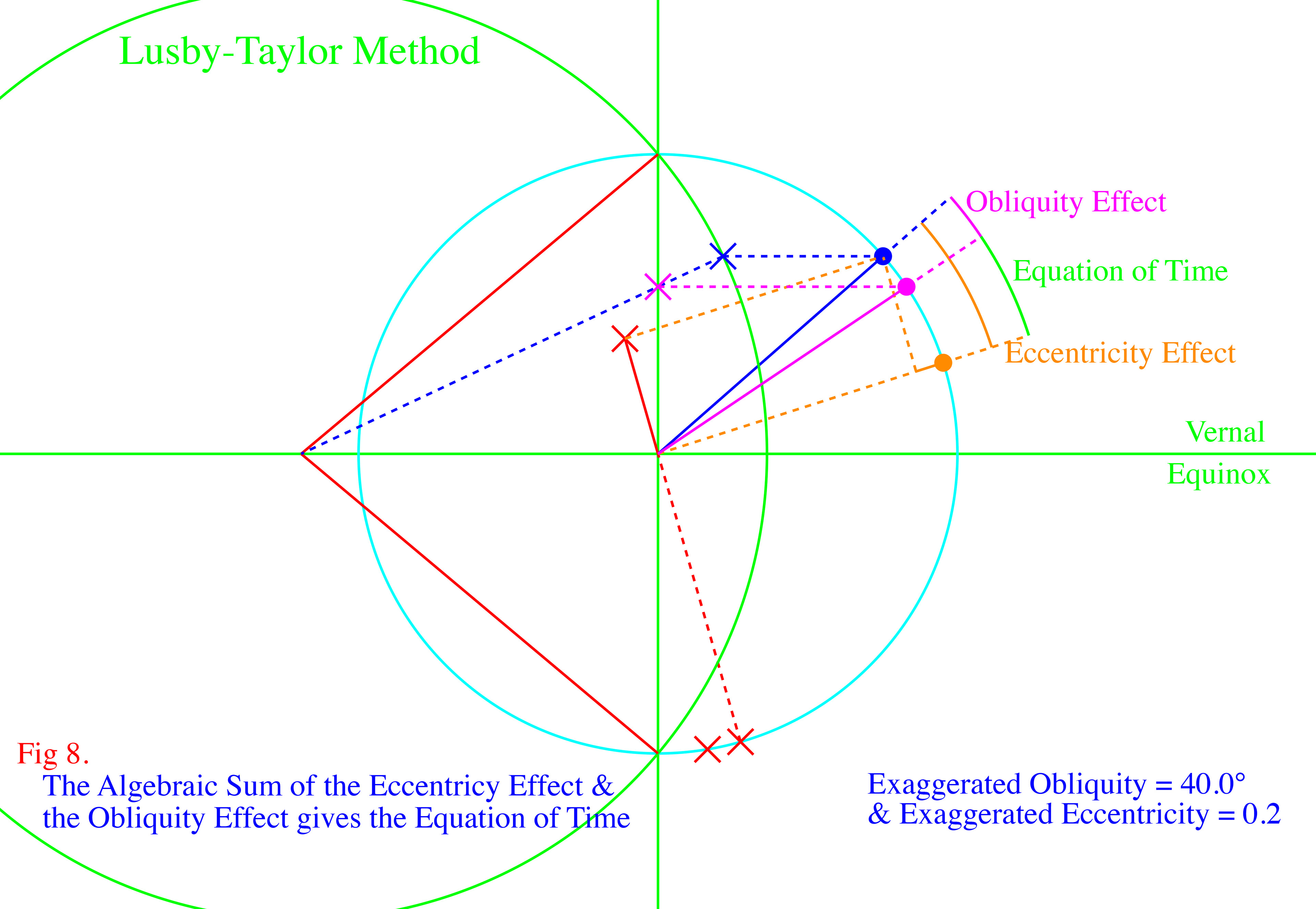
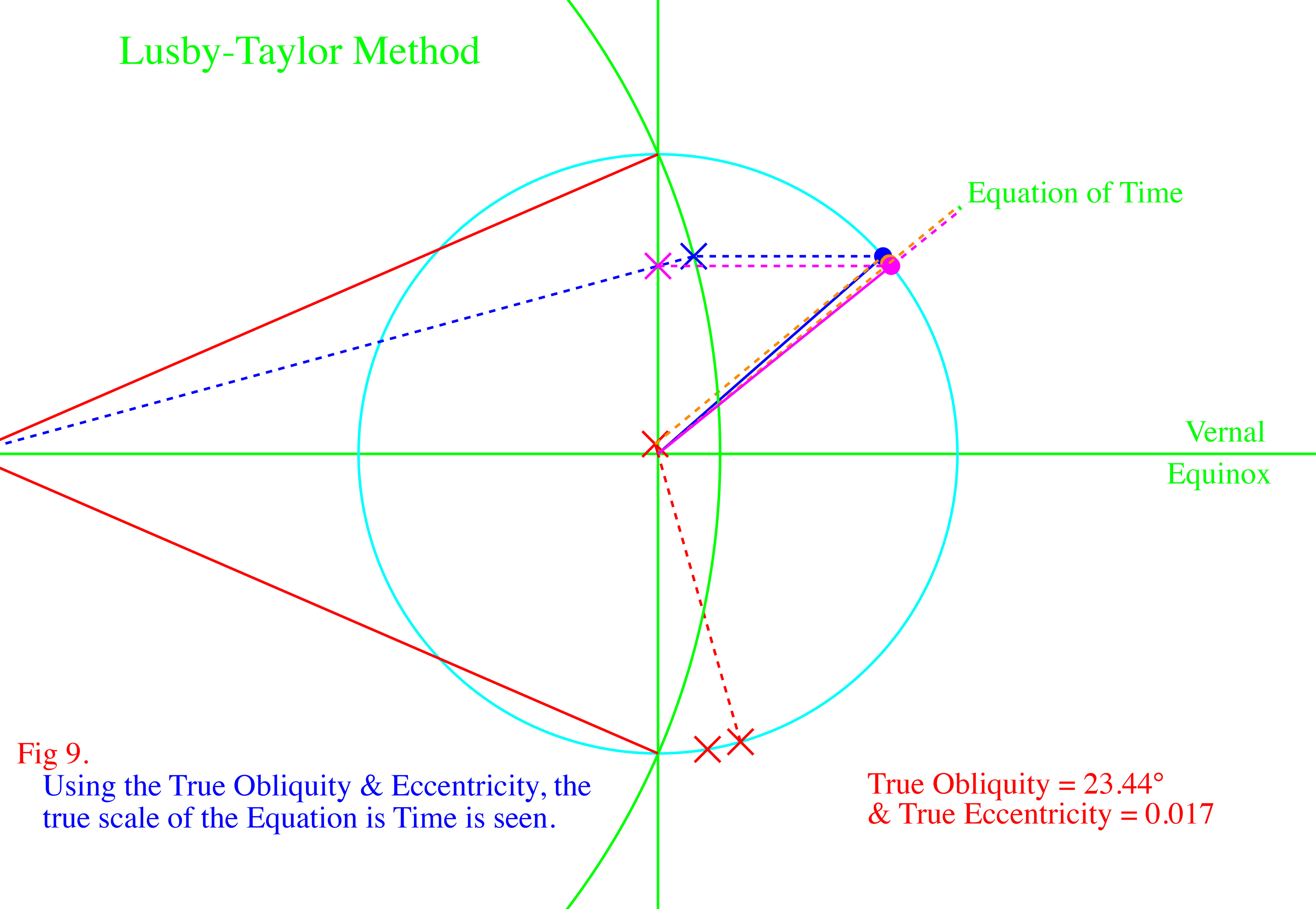
The images above show how the two components of the Equation of Time are geometrically produced. Click on the top, left image to enlarge, then use the right arrow,
The movies below show the geometry, both with exaggerated obliquity & eccentricity to make the geometry easier to see and with the true values. It must be borne in mind that a 1° arc on the circle is equivalent to 4 mins of time (360/24/60)