INTRODUCTON
Most Moving Hour Lines Dials are equatorial in nature where the hour lines are necessarily spaced at 15° per hour. Normally one would expect the noon hour line to be due north in the Northern hemisphere. By rotating the hour lines around the polar axis by an amount proportional to the Equation of Time and Longitude correction on the day in question, direct reading of civil time is possible. Commonly this is done using Pilkington's method - see Introduction to this section
EQUATORIAL DIALS
Pilkington's 1914 Sol Horometer
Brian Huggett - 2018 - Equatorial Heliochronometer
Singleton's Dial - note the Equation ring inset
Kurt Descovich - 2016 - Schwartenau Heliochronometer : Ref NASS Compendium 23:1 Mar 2016 : see also page on Gears
Dasypodius Society Dial ??? I do not understand this !
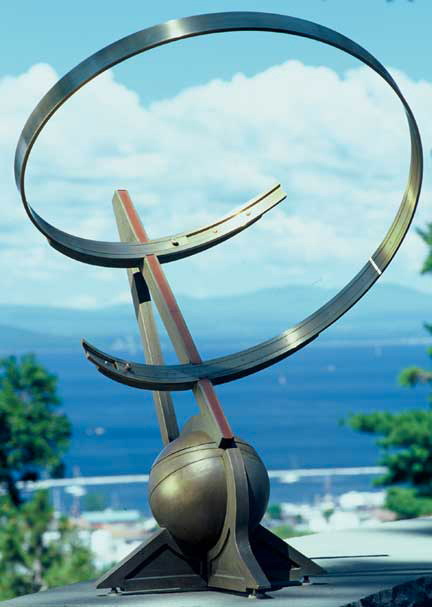
Bill Gottesman, www.precisionsundials.com - Renaissance dial
Bill Gottesman, www.precisionsundials.com - Renaissance dial
Bill Gottesman, www.precisionsundials.com - Renaissance dial
Carlo Heller's IcarusPortable Sundial - www.helios-sonnenuhren.de
Click on images to enlarge & view captions
A feature of Pilkington's method is that - for clarity - the month may be space out, as seen in Brian Huggett's dial above. This dial also separates the winter time months on the left from the summer time (DST) months on the right. There is some overlap to account varying dates of start/end of Summer Time.
THE CHARTRES DIAL
1882 Chartres dial by Ernest Bolle
marked to show the large portion of the dial that rotates around the gnomon
the Equation adjustment - the crank, bottom right turns the hour lines: the date is set to August 26th
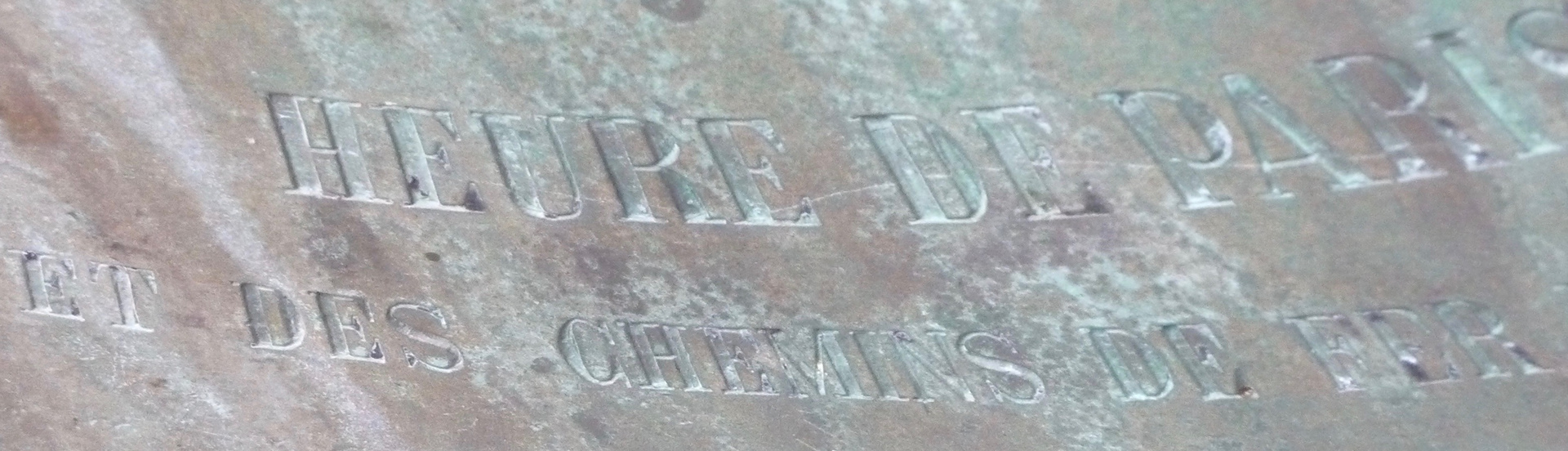
The dial indicates the change - spear-headed by the Railways - from Local Mean Time,e to National (Paris) Mean Time
Click on images to enlarge & view captions
NON-EQUATORIAL DIALS WITH MOVING HOUR LINES
With clever geometrical means, it is possible to convert conventional hour lines to read on an equiangular scale allowing Equation & Longitude correction. This is shown below in the Sawyer Equant Dials below - the stationary bronze conventional dial has a rotating stone plate with the equiangular hour lines ?? Other examples ??
Bill Gottesman www.precisionsundials.com, Sawyer Equant Dial : ref BSS Journal, Jul 1991
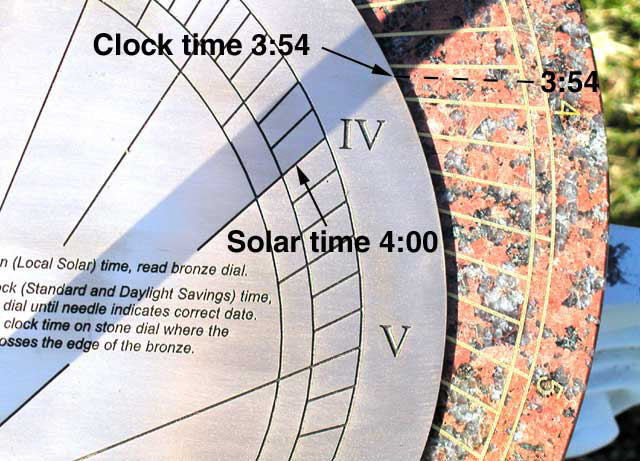
Bill Gottesman www.precisionsundials.com, Sawyer Equant Dial : ref BSS Journal, Jul 1991
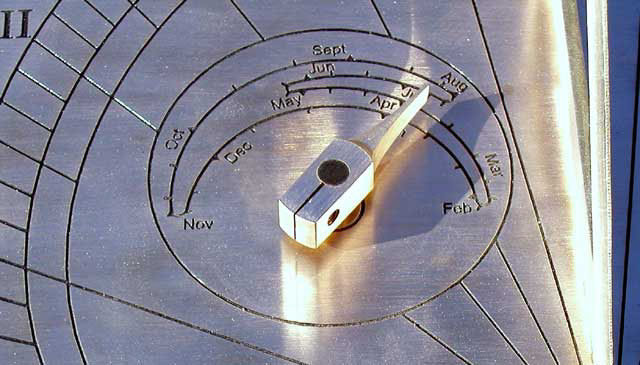
Bill Gottesman www.precisionsundials.com, Sawyer Equant Dial : ref BSS Journal, Jul 1991
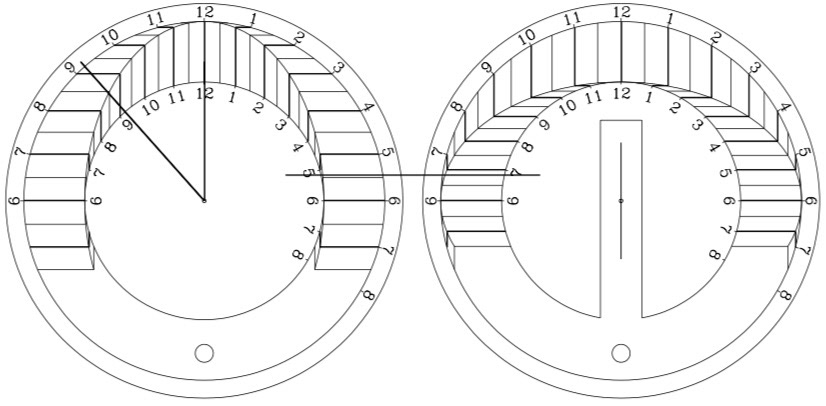
Frederick W. Sawyer III - A self-orienting latitude-independent analemmatic equant dial design - ref NASS Compendium v10(4), Dec 2003
Homogeneous Analemmatic Sundial - Hendrik Hollander - www.analemma.nl - ref NASS Compendium 15(2), Jun 2008
Homogeneous Analemmatic Sundial - Hendrik Hollander - www.analemma.nl - ref NASS Compendium 15(2), Jun 2008
Mac Oglesby's example of F.Sawyer's design : ref Time In A Perfect Round - NASS Compendium v8(3), Sep 2001
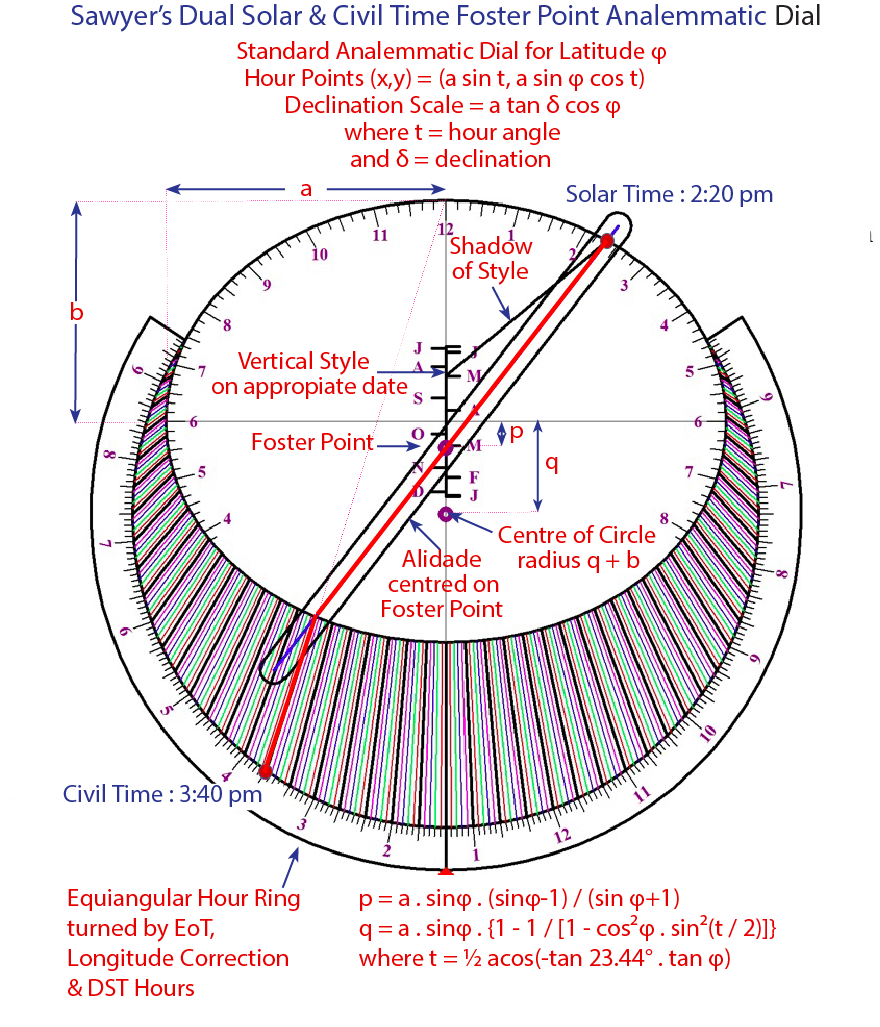
Sawyer’s Dual Solar & Civil Time Foster Point Analemmatic Dial : adapted from NASS 2017 St. Louis Conference.
Click on images to enlarge & view captions