. Many of the monochrome illustrations below have been taken from: "Some Outstanding Clocks over Seven Hundred Years" by H. Alam Lloyd, Leonard Hill Books, 1958. Or from: "Thomas Tompion, His Life & Work" by R.W. Symonds, B.T. Batsford Ltd, 1951
EQUATION CORRECTIONS - Part 1
a) PRINTED TABLE OF THE EQUATION ATTACHED TO (OR SUPPLIED WITH) A CLOCK OR WATCH

The clockmaker, Thomas Tompion's Equation table of 1683. Some 12 years later, the first Astronomer Royal, John Flamsteed, wrote to Sir Isaac Newton "Tompion's a true table of equations, but made for a particular year perhaps, fits not the present" !

One of two of John Harrison's personal regulators, with Equation Table in his own hand, printed on pendulum door. This clock was set, not by the sun, but by the stars viewed between Harrisson's door post and his neighbour's chimney.

Detail of Equation Table

Watch Paper. In the 18thC, many pocket watches would be supplied with such cut-out papers that could be folded to fit inside the each of the watch

Watch Paper. In the 18thC, many pocket watches would be supplied with such cut-out papers that could be folded to fit inside the each of the watch
Click on images to enlarge & view captions
b) AN UNKNOWN MECHANISM
One of the earliest recorded Equation Clocks was designed by the mathematician, Nicholas Mercator (not Gerardus Mercator who invented the map projection), and made by Ahasuerus Fromanteel (whose son, John, bought pendulum technology from Amsterdam to London) "Next day, to the Royal Society, where one Mercator, an excellent Mathematician, produced his rare clock and new motions to perform the equations..." wrote the diarist John Evelyn on 18 August 1666.
This may or may not be the clock described in c) below
The clock was also described thus:
c) CLOCKS WITH A MANUALLY ADJUSTED HOUR RING
The first clearly known step in mechanically adjusting a clock was from Ahasuerus Fromanteel (1607–1693), whose son brought Huygen's pendulum technology from Amsterdam to London about a year after Huygens published his invention. The widely publicised fact that Huygens invented the pendulum clock is almost certainly untrue. What he did invent is the crutch which connects the pendulum to the escapement. He also understood the circular error in pendulum, which eventually led the the adoption of the long seconds pendulum only swinging through a few degrees and the Clement's Anchor escapement.
Fromanteel's manually adjusted minute ring ca 1680
In the clock face, above, the outer minutes ring, the small upper seconds ring and the small lower hour ring are all manually adjustable for the EoT (using a printed table) by insertion of a pin into the small holes (dark dots in the image). There was a friction fit for the adjustable rings . Note, for example, on the outer minutes ring, the small 12 o'clock diamond is aligned at about 11:30.
d) JOHN SMITH'S TABLES TO KEEP CLOCKS AS CLOSE AS POSSIBLE TO SOLAR TIME
the author is grateful to Prof Frederick W. Sawyer III for the information in this section.
John Smith C.M. (1650 - 1730) was a colourful character. He was a clockmaker, hence the C.M. after his name. He wrote books. One was on the painting of sundials. Another extolled the heretical Socinian Controversy (by order of Parliament, these books was banned, ordered to be burnt and Smith forced to recant, Another on "The Curiosities of Common Water or the Advantages therefor in Preventing and Curing many Distempers". This book went to 10 editions and was published in translation in both Germany & France!
His last books, however related Horological matters - especially to the lack of acceptance of mean time. He published a number of works on the Equation of Time. The last of these, in 1694, elucidated the 10 Rectifying Days of the year on which one would need to adjust one's pendulum clock so that the clock would always indicate the time within 3½ minutes of Solar time. The title page of his book contains .... "With TABLES of EQUATION, and Newer and Better RULES than any yet extant, how thereby precisely to adjust ROYAL PENDULUMS, and keep them afterwards, as near as possible to the apparent (= Solar) Time.

John Smith's Book
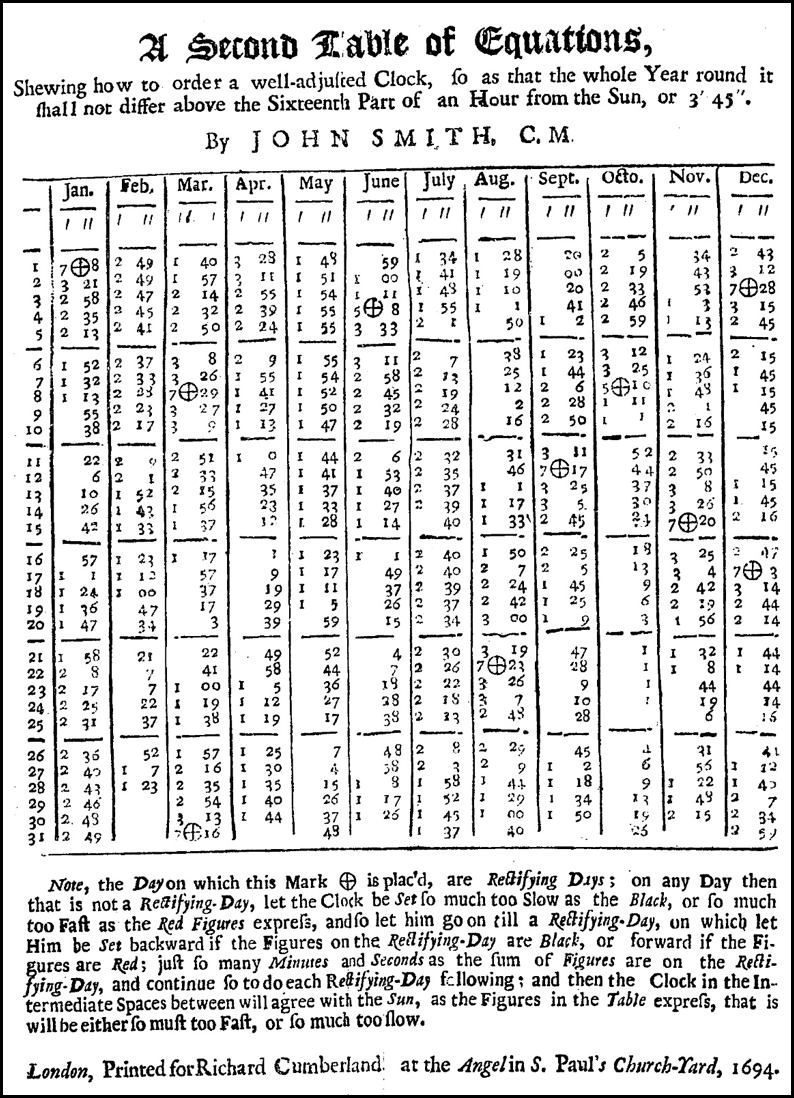
His Equation Table and the days on which rectifying had to occur
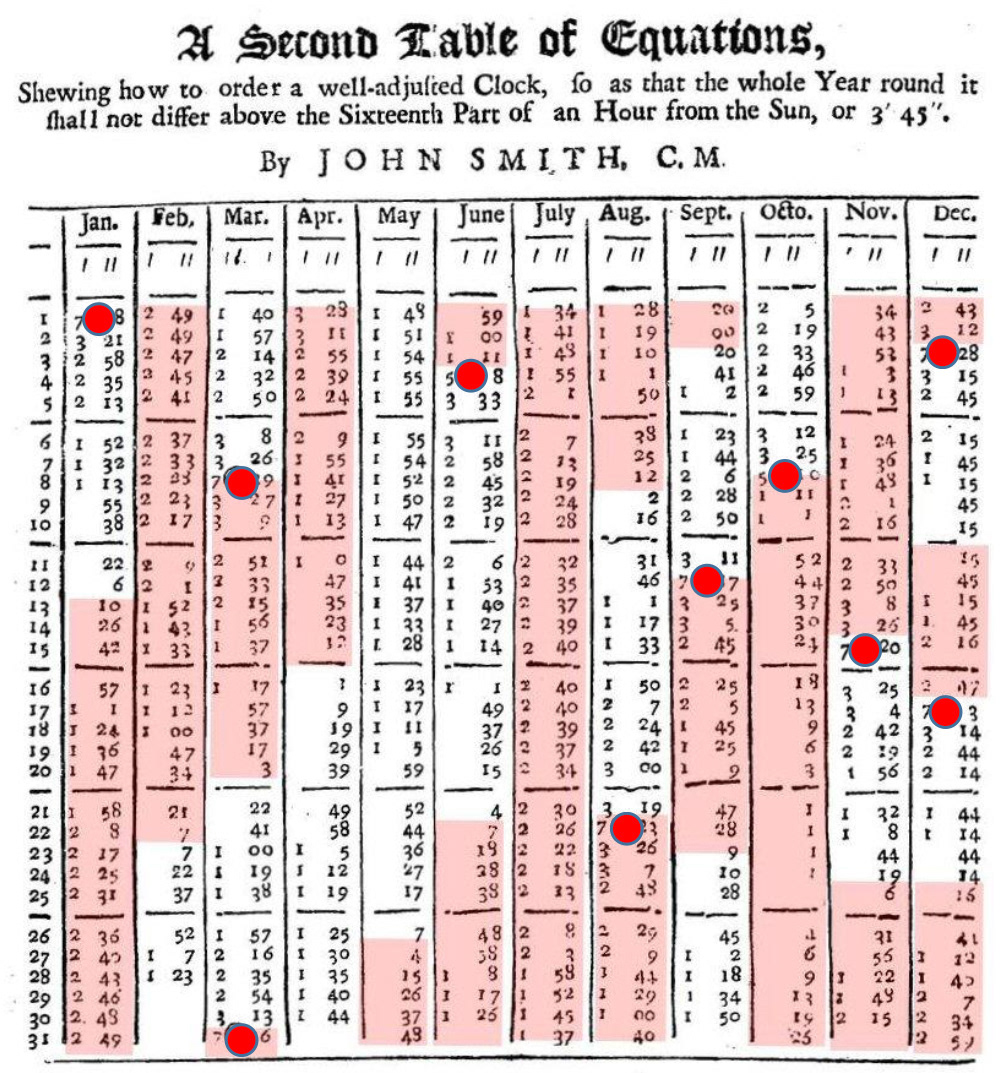

Rectification Instructions
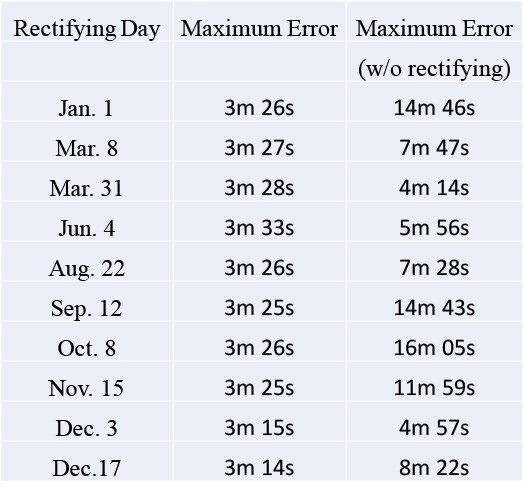
Table showing clock errors with and without rectifying.
Smith's method, if applied correctly, would means one's clock was always with 3¾ minutes from True Time
Recent re-working of John Smith's ideas by Fred Sawyer give a slightly better picture - in Gregorian dates. On Jan 1st, one sets the clock to equal Solar Time and then offsets it back by 7min 9 secs, etc. (see below). The clock will always be with 3½ mins of Solar Time
e) VARIABLE PENDULUM LENGTH
Joseph Williamson - who worked for the famous clockmaker Daniel Quare, in the letter that follows suggests that he was father of all Equation mechanisms. The letter was written to the Royal Society in order protect his name, He does however claim "I have made others for Mr Quar(e), which showed Apparent Time by lengthening and shortening the Pendulum in lifting it up and setting it down again, by a Rowler somewhat in the form of an Ellipsis, through a slit in piece of brass, which the spring at the top of the pendulum went through". Manual adjustment of a pendulum by moving the suspension spring through a slit was a common method used later to adjust clocks for temperature variation or wear & tear.



Letter from Joseph Williamson asserting his claim to have invented variable length Pendulum Clocks
Williamson's Variable Length Pendulum Mechanism
The following is a quotation on Variable Pendulum Clocks from the Encyclopédie
edited by Denis Diderot and Jean le Rond d'Alembert in the 18th century.
Father Alexandre's year wheel carries an ellipse on which rests a lever that carries the pendulum, suspended by a spring that fits closely through a slit in a cock, like conventional seconds pendulums. The spring can rise and fall in the slit; the cock is the center of oscillation, and it is mounted on the movement plate. To produce the apparent variations of the sun, Father Alexandre makes the pendulum longer and shorter by means of the ellipse; its diameters are determined in relation to the lengthening or shortening the pendulum requires in order to gain or lose a given amount in 24 hours. He gives extensive details on the subject on p .147 of his book. His theory certainly has the merit of simplicity, but to endorse it we must ignore its inherent practical disadvantages. A single error brings the whole structure down; the slightest error in the curve will produce a noticeable variation in the hands. Assume that inaccuracy in the ellipse makes the pendulum too short by 1/12 ligne; it will gain 12 seconds in 24 hours, etc., every beat during that time will be shorter than necessary, and this error multiplied by the numbers will give 12 seconds for just 1 point, and the same for every day. Moreover, this method is not practical with today's heavy pendulums, whose virtues have been well demonstrated in our time by M. de Rivaz. Finally, I do not see the advantage of a pendulum that divides time into unequal parts only. However, it was appropriate to mention this design, for the understanding it gives of the whole matter of equation; in addition, I am convinced that knowledge of all kinds of mechanisms is a great help in obtaining certain results in other constructions, even though they have no obvious connection with what inspired the initial idea. Nothing must be overlooked regarding the mechanical arts, but we must always assume understanding in the person who makes a new application to other objects.
translation from https://quod.lib.umich.edu/d/did/index.html