FOURIER ANALYSIS
Any repeating value (for example the Eccentricity or Obliquity effects or the Equation of Time itself) can usually be broken down into a series of sine components.
In the context of the Equation of Time, it will not be necessary to look at more than a few of the harmonic terms. However in accurate astronomy, many hundreds of harmonic terms may be implied to define the position of, for example, a planet.
At the bottom of this page, there is an example of how one may extract harmonic components using a spreadsheet
The figure above shows the output from a Fourier analysis of the Eccentricity & Obliquity components, together with the Equation of Time, itself.
Looking at the Red bars - one sees that the Eccentricity effect is made up of a dominant 7.7 minute harmonic and an insignificant second harmonic of 0.08 minutes or 5 seconds. It is difficult to imagine an application where the second harmonic would need to be considered.
Next, - looking at the Green bars - one sees that the Obliquity effect has zero 1st, 3rd or 6th harmonics, because the effect cycles twice throughout the year. But, it has a large 9.9 minute 2nd harmonic and a less important 4th harmonic which has amplitude of 0.21 minutes or 13 seconds. For application in sundials, the 9.9 minute harmonic alone is sufficient. (The best accuracy one can obtain with a normal sundial is 30 seconds.)
Finally, the Purple Bars are for the Equation of Time itself.
For applications in advanced astronomical clocks three components are used. For optical sun-tracking devices, one might consider both the signals.
ANALYSIS OF THE ECCENTRICITY EFFECT
In the left image below, an exaggeratedly large value of the Eccentricity has been chosen. This shows that at least two harmonics would be required to simulate the true values Th image on the right, using the true value of the eccentricity clearly indicates how close the true effect is to a single sine curve.
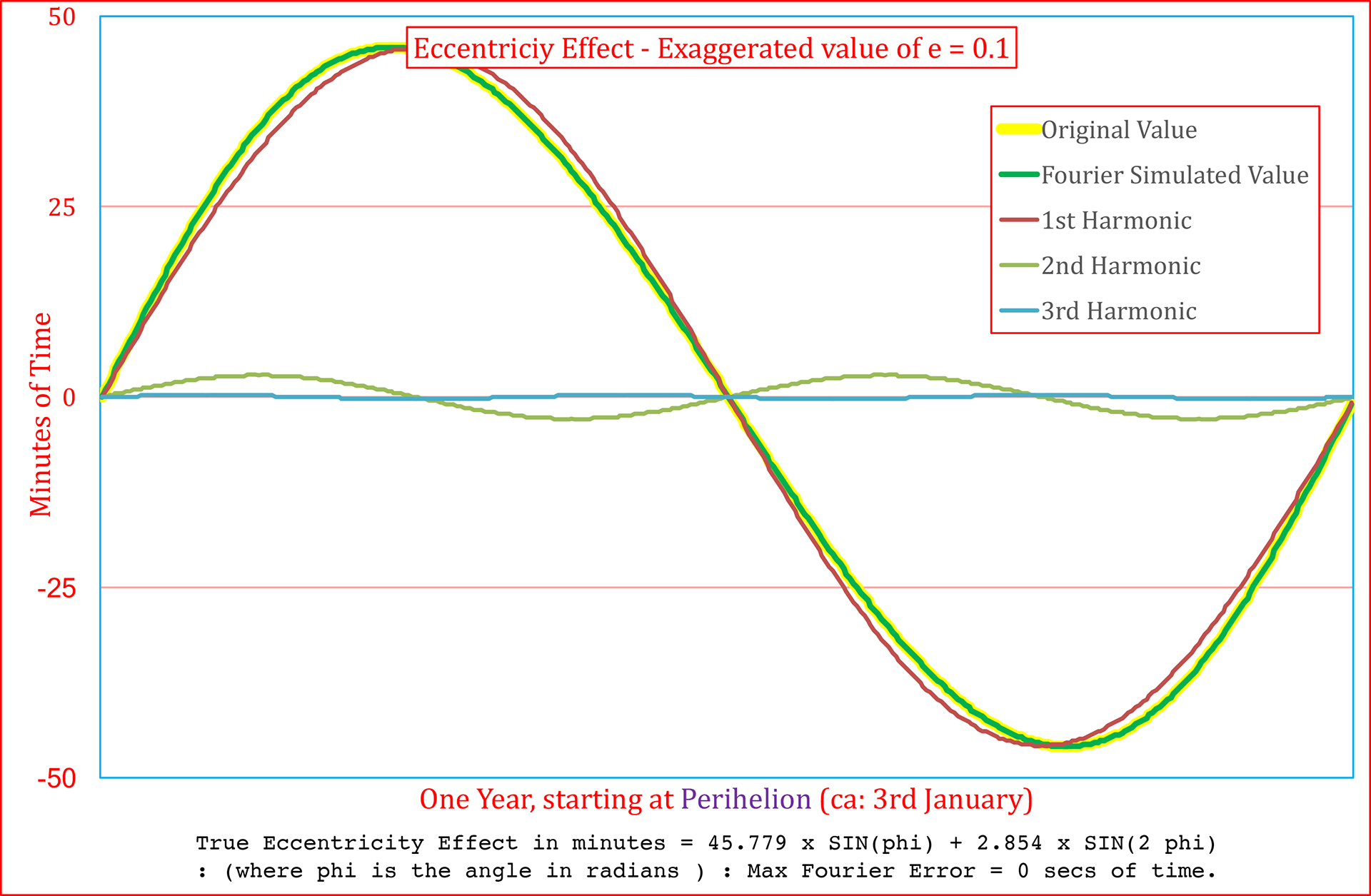
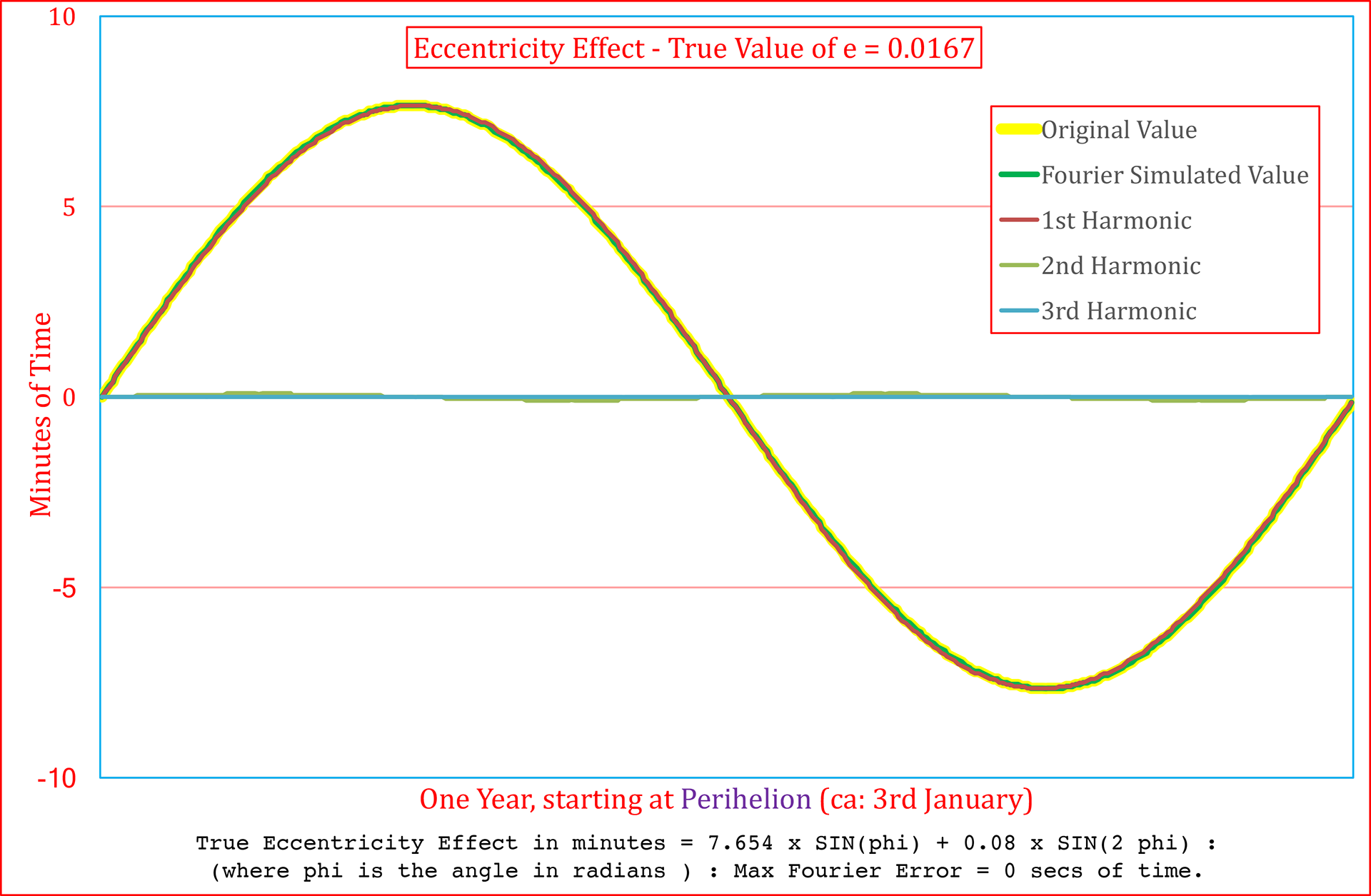
ANALYSIS OF THE OBLIQUITY EFFECT
As above, an exaggeratedly value of the Obliquity has been chosen. This shows that this effect is more complex than the Eccentricity effect. The true curve is arc tangent ( tan[dynamical mean longitude] x cos[Obliquity]). At least two harmonics would be required to simulate the true values The image on the right, using the true value of the eccentricity indicates that, except if great accuracy is required, a single harmonic would suffice.
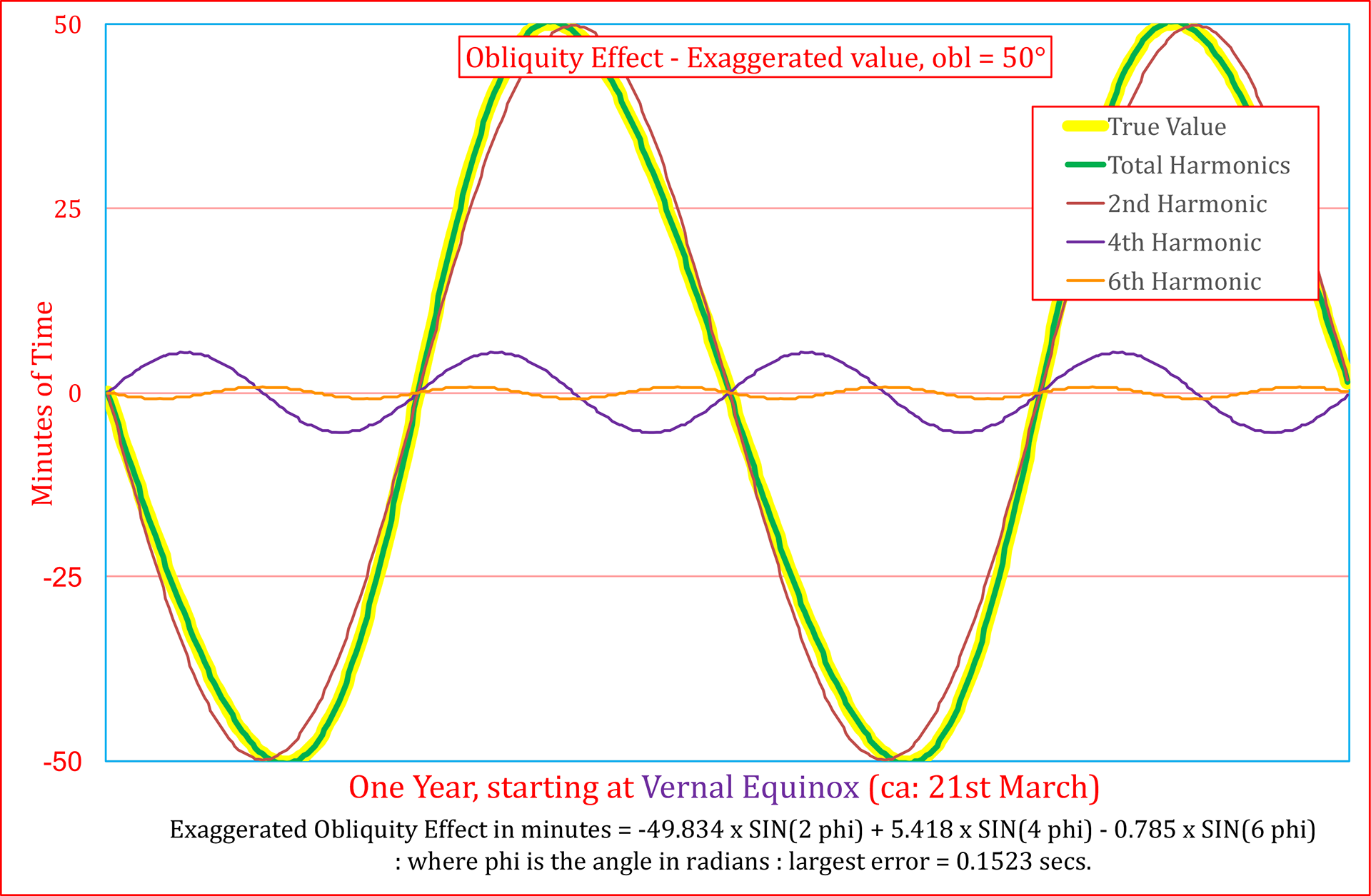
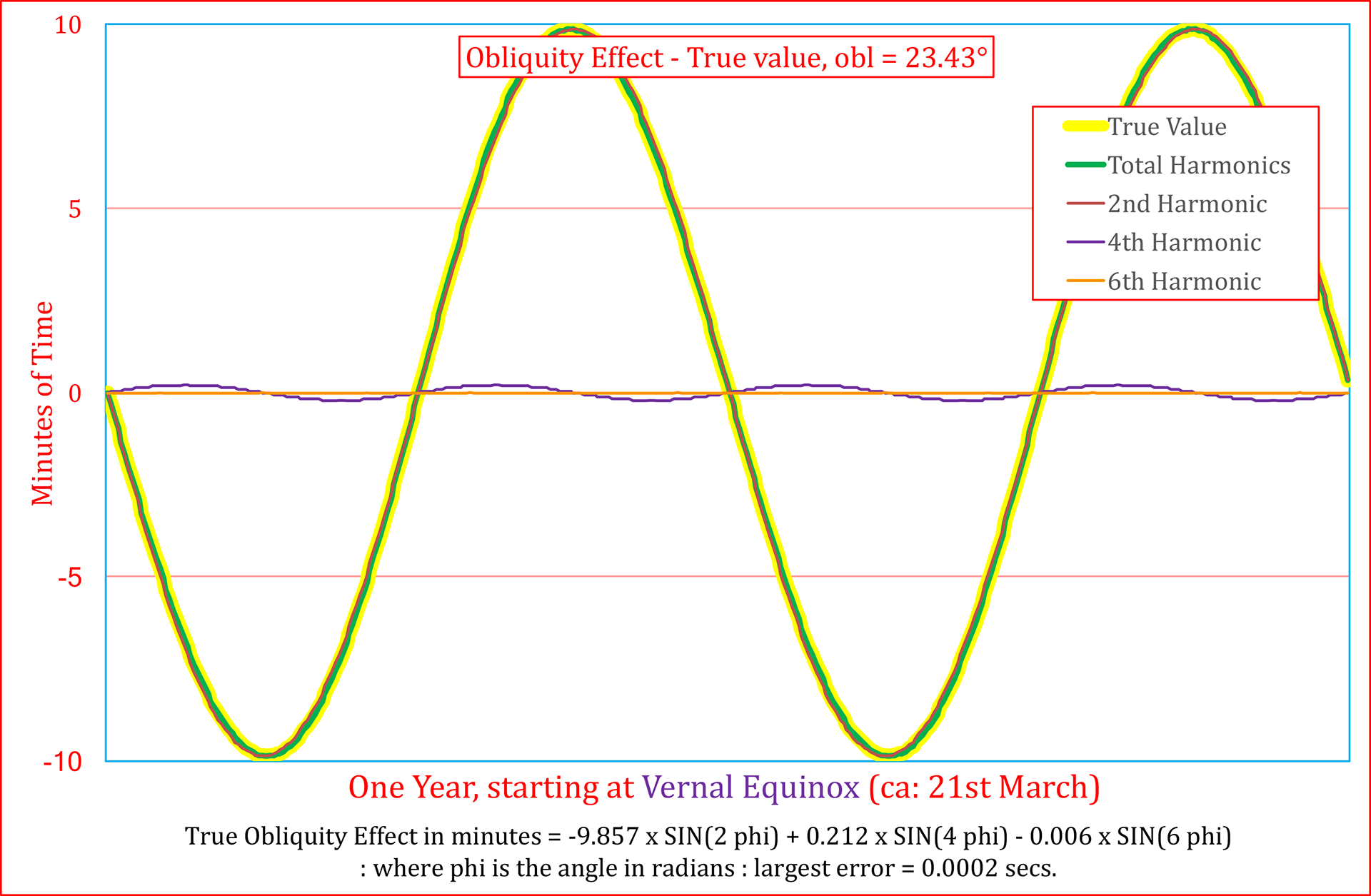
THE COMBINATION OF THE TWO EFFECTS
Unfortunately one cannot just add the two components together, since on has its origin at Perihelion and the other from the Vernal Equinox. However a Fourier analysis of the whole is shown below, together the accuracies achieved, depending who may terms are chosen.
EXAMPLE OF HOW TO PERFORM A FOURIER ANALYSIS
This example uses just 25 values of the Equation of Time, extracted from an high class astronomical program. These are the input in Column 2 .
Above is a simple spreadsheet example, showing how easy it is to perform a Fourier analysis with just 25 data points. With more data points, ones get a better result.
Input
1. 25 equally spaced dates over a 365 day year. The dates are every 14.6 (= 365 / 25) days. Note that the list does not include the end of the year.
2. EoT : The corresponding values of EoT for the above dates were taken from the MICA program from the US Naval Observatory
3. Av : The average of the 25 EoT values
4 Step : Array of 25 steps from 0 to 24
5. θ : The phase of each step = radians (Step/25) = π x Step / (180 x 25)
Harmonic 1
6. n : The harmonic number = 1
7. n × θ : the harmonic number × the phase
8. EoT × sin(n × θ) : the sine component
9. EoT × cos(n × θ) : the cosine component
10. p : 2 × the average of the sine components
11. q : 2 × the average of the cosine components
12. A = √(pxp + qxq) : the harmonic amplitude
13. φ = atan2(p, q) / n : the harmonic phase
14. H1 = A × sin[n ×θ + φ] : the harmonic component
Harmonic 2
repeat steps 6. to 14, but with n = 2, to obtain H2
Output
15. Av + H1 + H2 : the Fourier output is Av + H1 + H2
16. the output is compared with the input - converted to seconds