Dual Cams
The 'purest' way to produce the EoT mechanically is with 2 cams, the output of which are added together. One cam turning once a year simulates the Eccentricity Effect. The other turning twice a year simulates the Obliquity Effect. For astronomical clocks, designed to work in the longer term, this has the added advantage that the Eccentricity cam can be driven once per Anomalistic year (the time from one mean perihelion to the next = 365.259 636 days). While the Obliquity cam can be driven twice per Tropical year (the time from one mean vernal equinox to the next = 365.242 189 days)
The output from each cam is then added with a 'wiffletree' or other mechanism (as shown in the following video.
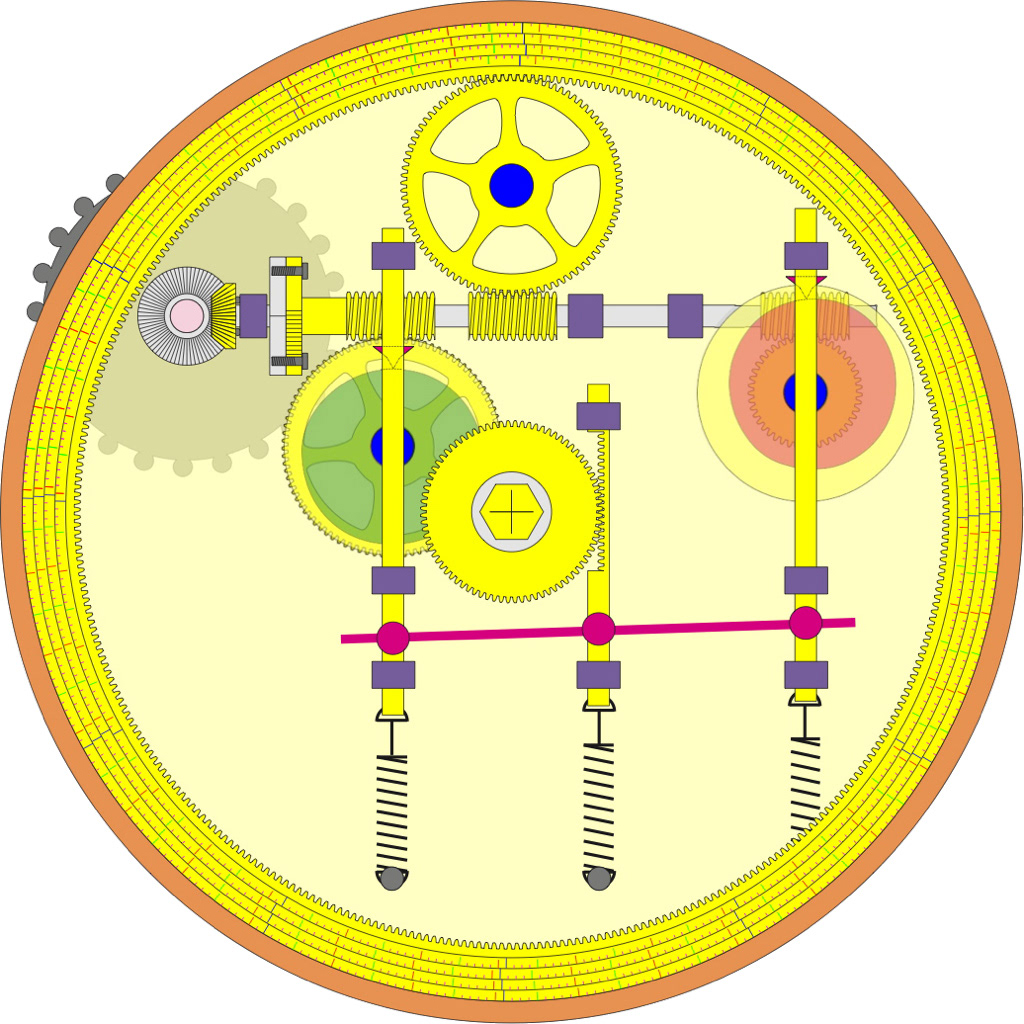
The author's Dual cam design (never realised). The green cam rotates once a year, the red, twice a year. The upper yellow gear drives a four-year leap year date setting ring
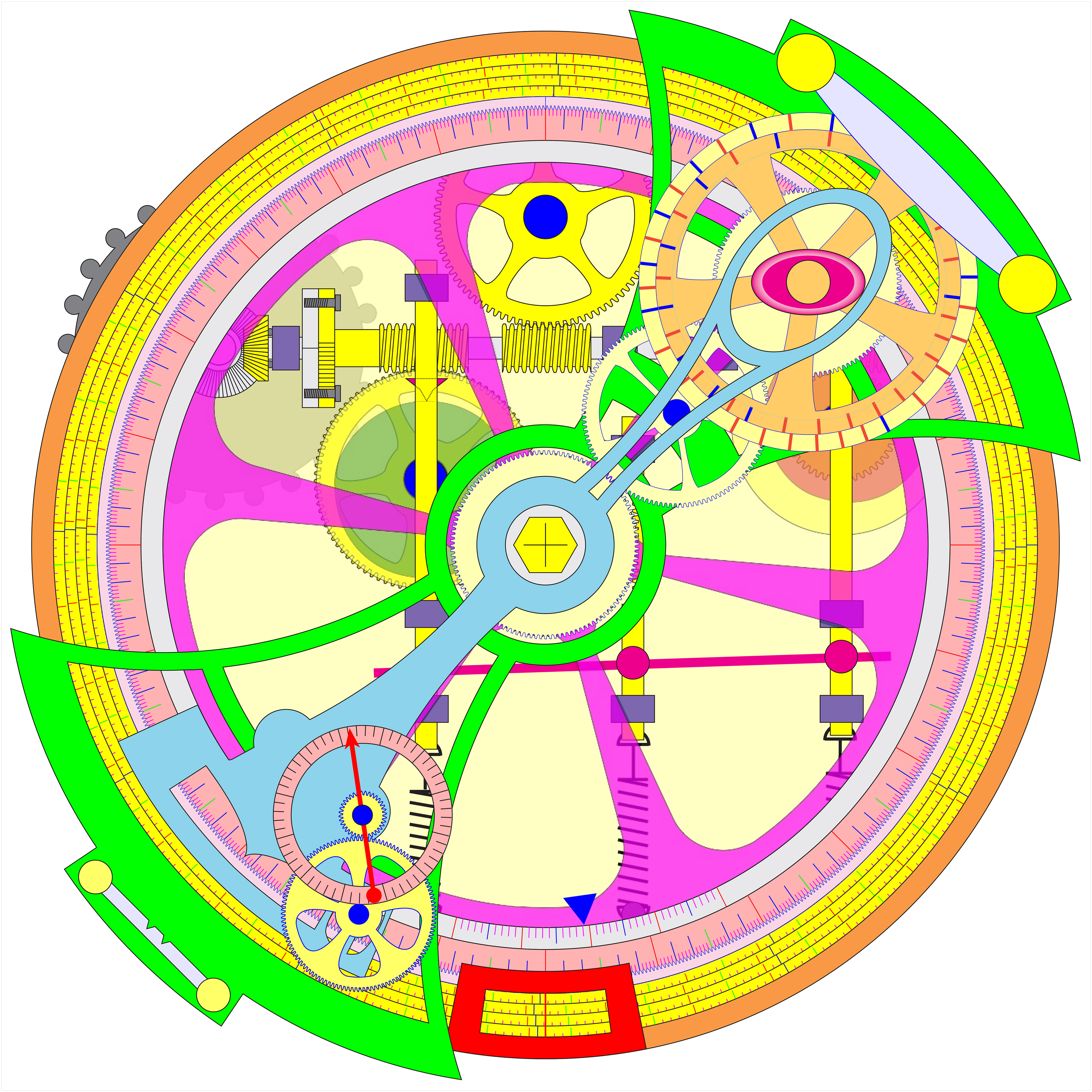
The same design, as left, with its centrally mounted lens-ed alidade. The blue potion was a refraction correction which is theoretically incorrect.
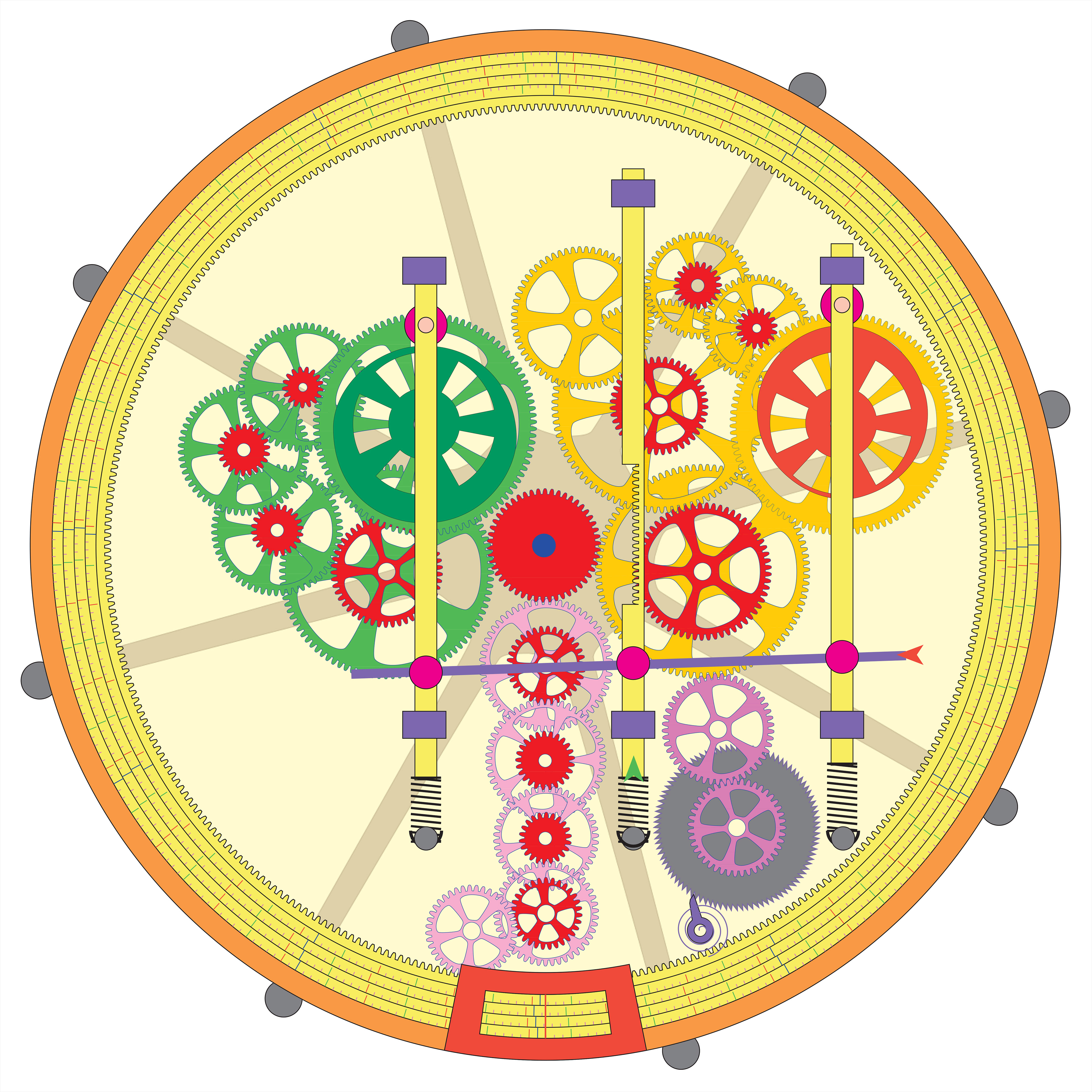
another of the author's unrealised designs. In this case the green cam is driven at once per anomalistic year, the red at twice per tropical year. The purple gears rotate the date setting ring at once per calendrical year
Click on images to enlarge & view captions
You can read a complete story of this unrealised dream below.... The description of the refraction correction is incorrect
Another double cam system can be found in Bill May's work. Here one cam sits inside another. This produces an effect similar to that of of two gears (see Gears page). The inner (circular) cam carries an eccentric pin that connects to the equatorial ring of a dial. The inner cam is carried eccentrically inside the outer ring. The inner cam is turned wide in the year (Obliquity effect) ; the outer ring once (Eccentricity effect)

Bill May - ca 2000 - Equatorial Dial

Inner cam carrying an eccentric pin driving the Hour ring

Outer ring and inner cam, showing month graduations - version 1

Outer ring and inner cam, showing month graduations - versions 2
Click on images to enlarge & view captions
SINGLE CAMS

Pilkington-Gibbs Heliochronometer - ca 1910 - (this dial, still in mint condition) was given to Commander Robert Peary, who first reached the North Pole by the Lord Chief Justice of England, who had previously adjudicated in the international dispute Arctic fishing rights)

the mechanical working of a Pilkington Gibbs - showing the cam and its follower, which is attached to the alidade
Click on images to enlarge & view captions

Bill May - 2000 - EoT profile directly driving the equatorial ring of his sundial

Bill May - 2000 - EoT profile directly driving the equatorial ring of his sundial
Click on images to enlarge & view captions