ON WHICH DAY OF THE YEAR IS THE LATEST SUNSET?
One might suppose that this would be on the Winter Solstice. But no - the time of sunset is when the sun is at zero altitude. This time in Civil Hours is given by the formula:
The formula shows that the duration of morning and afternoon are not equally dispursed around civil noon. Around the Winter Solstice, the value of the Sun's Declination is only changing marginally each day, while the Equation of Time is changing relatively rapidly. The effect of the changing EoT outweighs that of the changing declination. This leads to the day on which sunset is latest moveing away from the winter solstice and towards January (in the Northern hemisphere).
As one moves towards Equatorial Latitudes, the tangent of the Latitude trends towards zero and the timing of sunrise and sunset varies little throughout the year, but the EoT effect becomes signifiant, as shown in the graphs below. These show the time of Sunrise in Solar Time (Green) and in Standard Time = Local Mean Time (Cyan & Red)
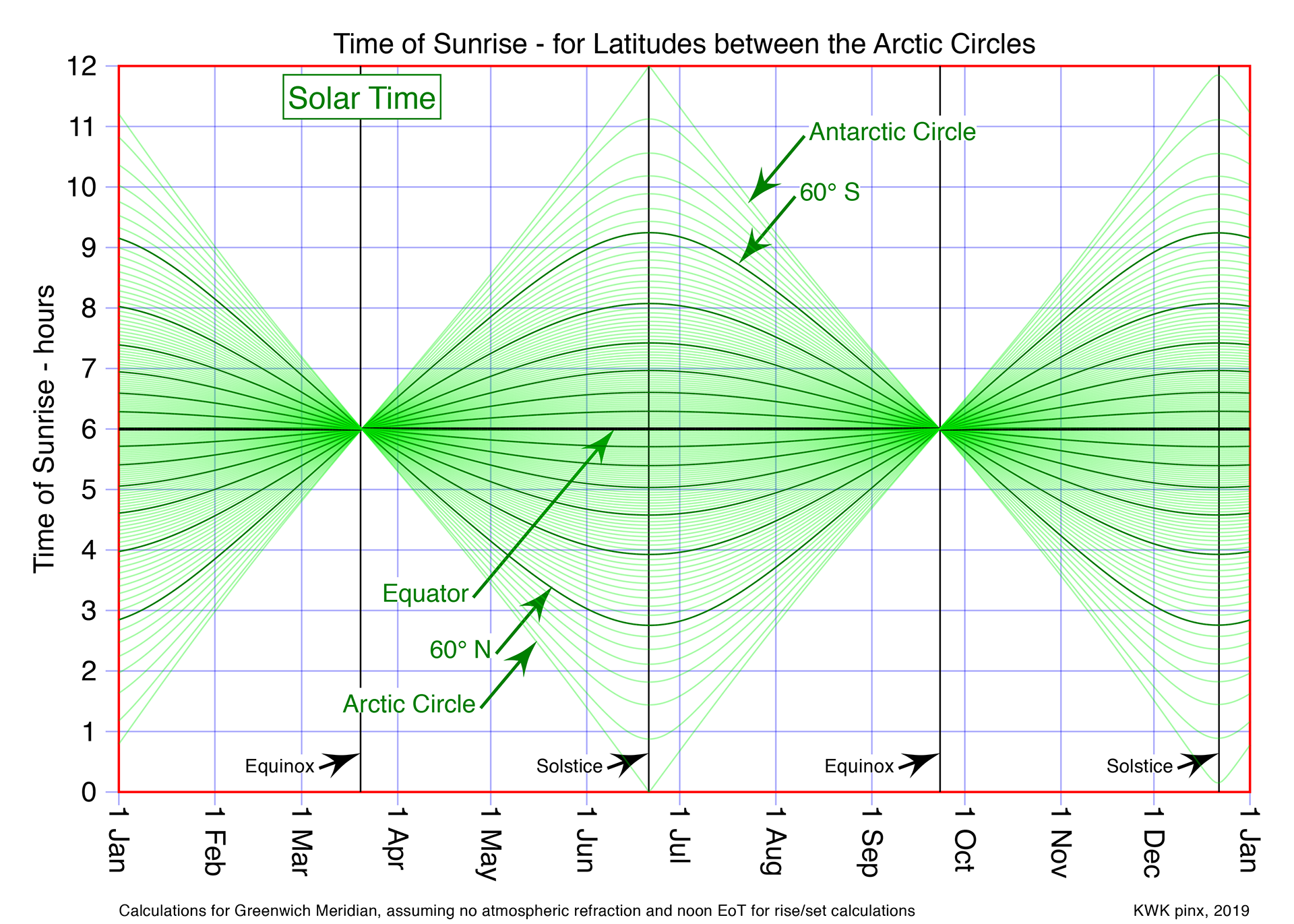
In the Solar Time Graph above...
Note 1: at the Arctic circles, there is a linear daily change, midnight to noon, from the summer to winter solstices;
Note 2: at the Equator, dawn is at 6:00 a.m. throughout the year.
Note 2: at the Equator, dawn is at 6:00 a.m. throughout the year.
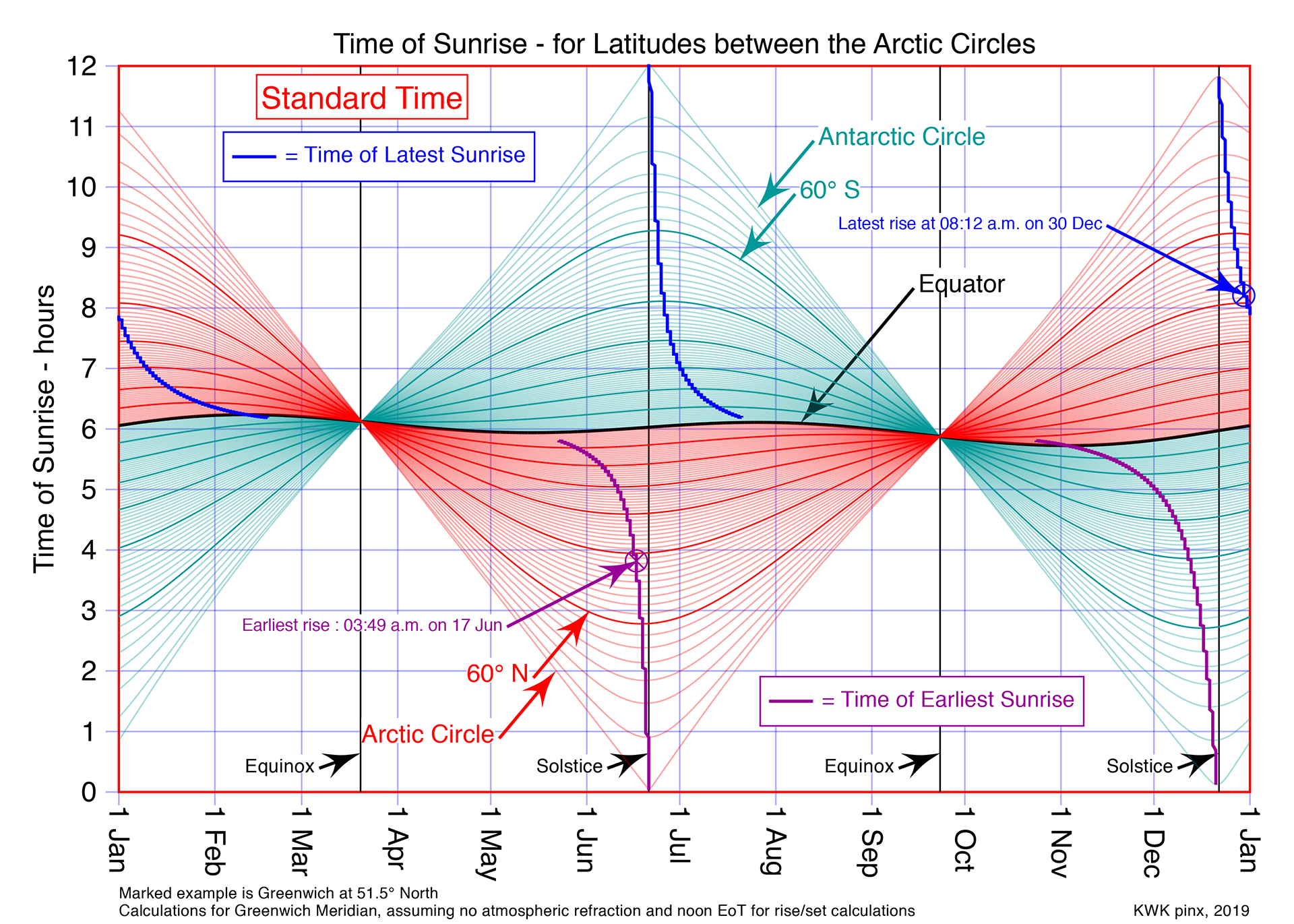
In the Standard Time Graph above...
Note 3: at the Arctic circles, there is no effect of the equation, so the linear daily change, midnight to noon, from the summer to winter solstices remains;
Note 4: at the Equator, the time of sunrise exactly reflects the Equation of Time - see the waves of the black Equator line. This is what one would expect bearing in mind that the solar time sunrise is the same throughout the year;
Note 5: at the marked example latitude (Greenwich), the earliest/latest sunrises are a few days away from the Solstices. While nearer the Equator, the difference from the solstices rise to almost 2 months.
Note 4: at the Equator, the time of sunrise exactly reflects the Equation of Time - see the waves of the black Equator line. This is what one would expect bearing in mind that the solar time sunrise is the same throughout the year;
Note 5: at the marked example latitude (Greenwich), the earliest/latest sunrises are a few days away from the Solstices. While nearer the Equator, the difference from the solstices rise to almost 2 months.
Another view of the effect of EoT on sunrise and sunset times can be seen in the following graph. Here the effect of the EoT can be seen as the twist in the curves around the Equator.
A GNOMONIST'S RIDDLE
You are sitting on a park bench reading the local newspaper. You have no timepiece, but there is a Sundial nearby. The sun is shining. How do you find the Standard Time?
Answer
Your local newspaper usually has the time of Sunrise and Sunset. Add together the time of Sunrise and Sunset, subtract 24 and multiply by 30 and you have the EoT and the longitude correction in minutes. Read the Sundial, apply the correction and you have the standard time. Add an hour in the summer.
A glance at the formula in the previous section will show why this is so, since adding sunrise to sunset cancels out the +/- trigonometrical part.
This method was well known in the 19th C, as shown below.
from Elementary Mathematical Astronomy by Barlow & Bryan 1893
ANALEMMAS ON OTHER PLANETS
The following taken verbatim from Bob Urschel's fascinating website - www.analemma.com
Permission being sought to duplicate
Of the nine planets in our solar system, seven of these (including Earth) exhibit the right orbital characteristics for the sun to form an analemmic curve throughout the planet's solar year. The two exceptions to this are Mercury and Venus. The length of day on these two planets almost matches the revolution time around the sun, thus the motion of the sun from one day to the next is not a smooth analemmic curve. In fact, the length of the day on Venus is slightly longer than its' solar year.
Mars
Jupiter:
Saturn:
Uranus:
Pluto
Saturn: