MECHANICAL POSSIBILITIES
Two broad categories of mechanical means are available to mechanically simulate the Equation of Time : cams or gears or a combination of both. The choice depends on the accuracy required and the space available.
Cams appropriately shaped provide the easiest and most compact method - typically used in Equation Clocks and Watches. Usually only a single cam is used, but two cams can also be employed.
Gears are more complex - but provide a more accurate, more interesting, visual and educational method - at the expense of complexity. EoT generation with gears is typical for Astronomical Clocks.
Mechanical methods with gears universally use that fact that the Equation of Time can be broken down astronomically or by Fourier Analysis into a series of sine curves. A sine curve is easy to generate with a gear. Usually the accuracy demands of the mechanism mean that only the first two harmonics of the Fourier series are used.
GENERATING A SINE CURVE MECHANICALLY
A rolling wheel can produce a sine curve, but we generally need a linear output. This is best produced by an epicyclic gear using the Tusi Coupling Method (invented by Nasir al-Din al-Tusi, the great Persian astronomer and polymath, in 1247). This requires an outer gear of twice the pitch diameter of the inner. The pitch diameter of the outer being the magnitude of the signal one wishes to produce
Description of the Tusi Couple - 13th C
The Tusi Couple - which is a special case of hypocycloid theory.
John Goodman's Simplified Tusi Couple. The second of three very short videos herein shows how gears of the same physical size can generate linear sine output of differing magnitudes.
ADDING TWO (or more) SINE CURVES
In the case of gears and double cams, it is necessary to add the the different sine components together. This can be done in three ways : (i) a differential adder (more gears), (ii) pulleys (iii) a whippletree
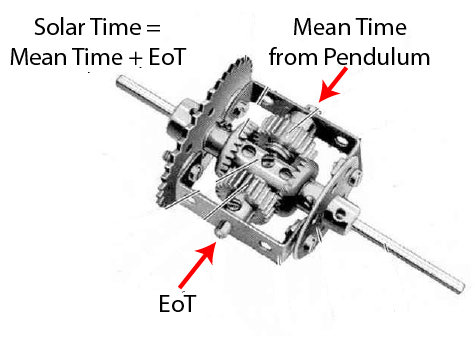
Differential Adder - commonly used to add EoT + Mean Time = Solar Time

Differential from 1930s Pouvillon watch

Pulley Adder, commonly used to add Eccentricity & Obliquity effects
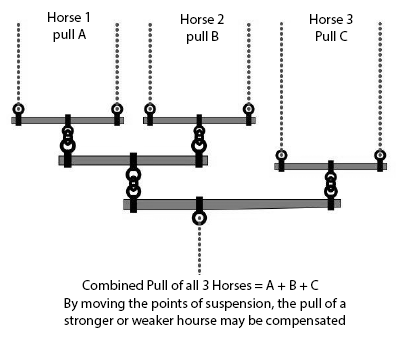
Wiffletree Adder
Click on images to enlarge & view captions