Nota Bene. We use a geocentric view in this discussion - as is still used by navigators with sextants. This is just a difference frame of reference than the 'real' situations with the Sun at the centre of the Solar System.
Firstly, to see how the Equation of Time is generated, we need to remember what is meant by the Mean Time, that is required by navigators and astronomers (refer to the page on Mean-v-Solar Time). Mean Time is based on the concept of the fictitious Mean Sun moving uniformly around the Celestial Equator, completing its circuit in one year. The Mean Sun's longitude is defined as zero at the Venal Equinox. The Earth, rotating once a day, will 'see' that the Mean Sun will transit over Greenwich at 12:00 hrs GMT.
Secondarily, we invoke a second imaginary sun to aid our calculations. This is the Dynamical Mean Sun, which moves uniformly around the Ecliptic once a year. The Ecliptic is at 23.5° to the Equatorial plane. The two planes intersect at the Vernal and Autumnal Equinoxs. The Dynamical Mean Sun and the Mean Sun go around the respective great circles once in a year and are thus travelling at exactly the same speed.
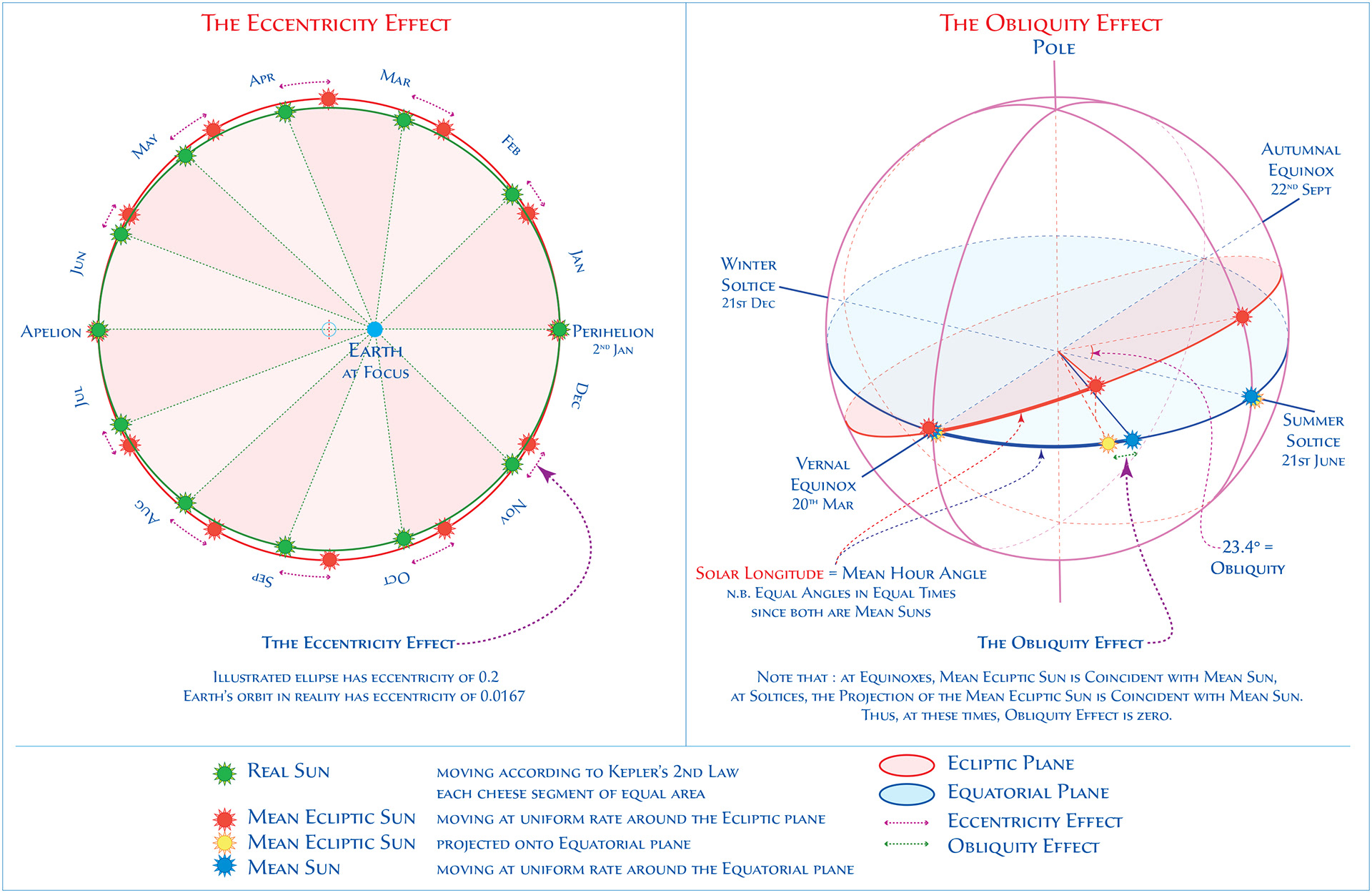
THE ECCENTRICITY EFFECT
The True Sun does not move uniformly around the Earth. In the 18th C, Johann Kepler worked out the orbit must be an ellipse and that the Sun would move faster when it was closest to the Earth, (at so-called perihelion). Kepler, in his 2nd Law, stated a radius vector joining any planet to the Sun will sweep out equal areas in equal lengths of time. The following video illustrates this effect. It shows the celestial sphere, sliced through the ecliptic plane. For the sake of clarity, an ellipse of eccentricity (egg-shapeliness) of 0.4 is used. In comparison, the earth's eccentricity is a tiny 0.0167.
When the video runs, it will show...
the Yellow 'True Sun' sweeping out the yellow cheese-shaped wedge. This is travelling around an ellipse, going faster and slower according to Kepler's 2nd Law
the Red 'Mean Dynmamical Sun'. sweeping out the red cheese-shaped wedge This is an imaginary sun travelling around the Ecliptic at a uniform speed.
Kepler's Law states that yellow and red wedges must be of equal area. The angular distance between the True and Dynamical Mean sun is the Eccentricity Effect of the Equation of Time - which is large, in this case, since a very large eccentricity was chosen.
The video starts at Perihelion.
The next video is the same except the true eccentricity is used. Note that the angular difference between the two suns is now very small. However, from the Earth spinning 360°/day at the centre of the celestial sphere, 1° angular difference equates to 4 minutes of time (= 24 x 60 / 360).
The next video shows the same once more, but this time shows the whole celestial sphere and plots the Eccentricity Effect, starting at 1st January, in minutes of time (converting angular distances to time at the rate of 4 minutes/degree. )
THE OBLIQUITY EFFECT
The second component of the Equation of Time is the Obliquity Effect. Since we are basing our time keeping on uniform movement around the Equator, we must project the position of the Dynamical Mean Sun down onto the Celestial Equator. Uniform movement around the Ecliptic does not translate into uniform movement when projected onto the Celestial Equator. This is shown in the following video. In order to compare it the uniformly traveling Civil Mean Sun. To amplify the effect, a vale of 40° has been chosen for the Obliquity (the angle between the Ecliptic & Equatorial planes) rather than the true value of 23.4°. The video runs for a year, starting from the Vernal Equinox.
This video is the same as before, but with the true value of the Obliquity, and running from 1st January.
ADDING THE ECCENTRICITY & OBLIQUITY EFFECTS TO GIVE THE EQUATION OF TIME
The following video shows how the final shape of the Equation of Time can be deduced by adding together the Eccentricity Effect and the Obliquity Effect
The final video shows that one does not have to invoke the Dynamical Mean Sun if one knows the Right Ascension of the Sun, which is the arc from the Vernal Equinox around the Equator to the projection of the True Sun onto the Equator. The amount of the projection is Declination of the Sun.
One should note, however, that in order to calculate the Right Ascension of the Sun (by most non-professional means), one needs to use the concept of the Dynamical Mean Sun.
In the simulations above, which were generated by the free software Persistence of Vision (or POV_Ray), some liberties have been taken the ease the calculations. Viz: the length of the year was taken as 365 days; the time from Jan 1st to Perihelion was taken as 3 days; the time from Jan 1st to the Vernal Equinox was taken as 80 days. Within these constraints, the simulations are physically correct (or so I hope).
SUMMING UP
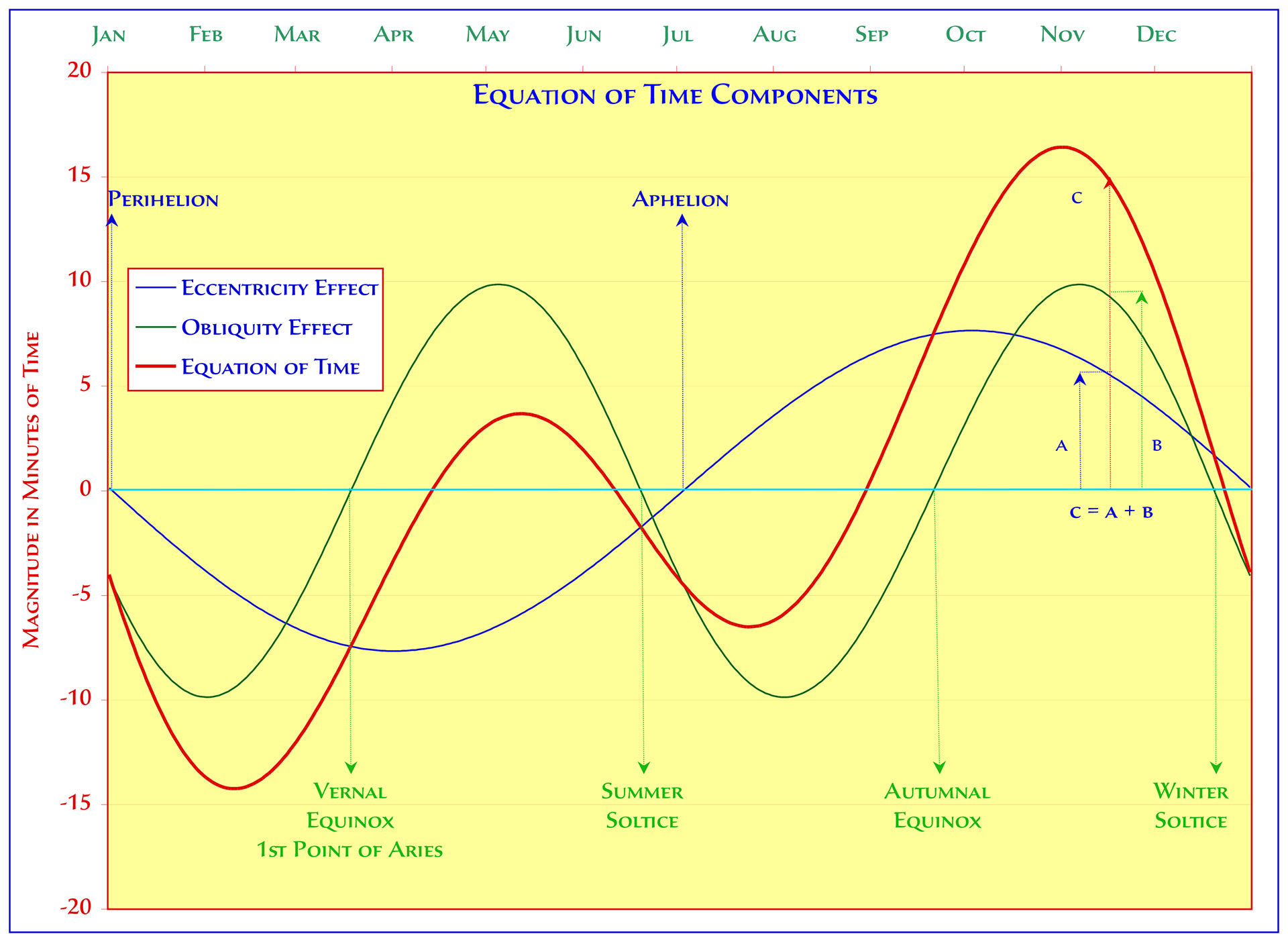
Click to Enlarge : the Left graph uses the Astronomical Convention for the EoT