MORE WORK NEEDED ON THIS PAGE
CAVEAT
Tables which provide the Equation of Time (e.g. on the Web) and pertain to be 'accurate', should always quote to which time zone they apply. Such tables usually give the EoT values for noon. But noon in Seattle is hours different from noon in Bombay. When the Equation of Time is changing rapidly - some 30 secs/day around Christmas - tables created for one time zone will be incorrect by 15 seconds on the other side of the world.
THE LEAP YEAR CYCLE
The tropical year is about 365¼ days and our calendrical cycle usually runs on a 1461 day cycle (3 x 365 + 366). Thus the 12:00 noon EoT one year will be the 18:00 pm EoT the next.
LONG TERM TRENDS
There are many reasons why the Equation of Time varies between one year and the next. The value of the Equation of Time is dominated by two variables - the Eccentricity & Obliquity of the Earth's orbit - (see section 'The Components of the Equation of Time'). Over the very long term, the movement of perihelion around the ecliptic becomes important. Since we count our days from Jan 1st. we need to see ...
(a) how our calendrical system interferes with the time from Jan 1st → Vernal equinox & Jan 1st → Perihelion.
(b) the actual values of Eccentricity & Obliquity over time
Thus, as shown below, although the time between Jan 1st and the Mean Value of the
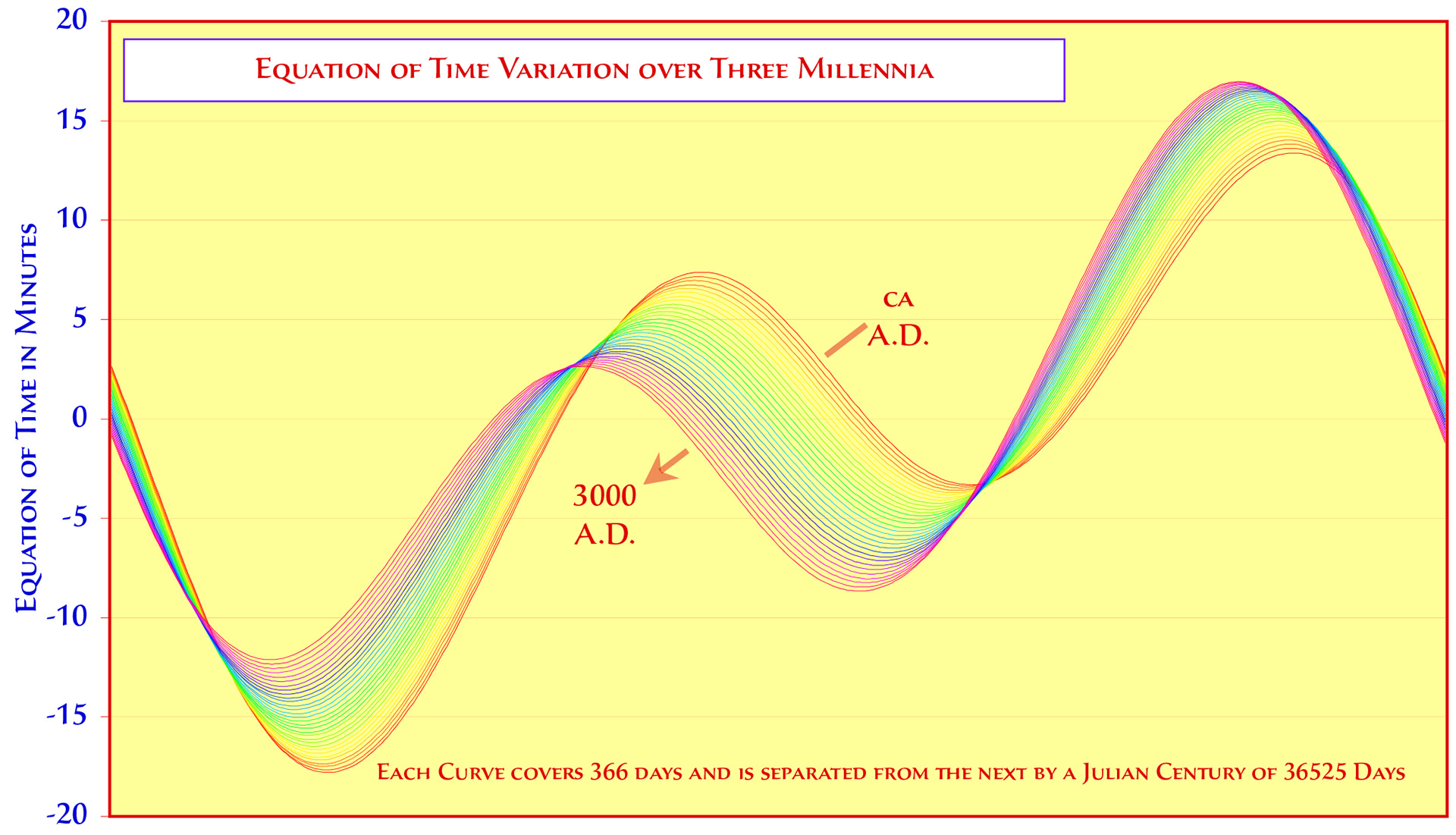
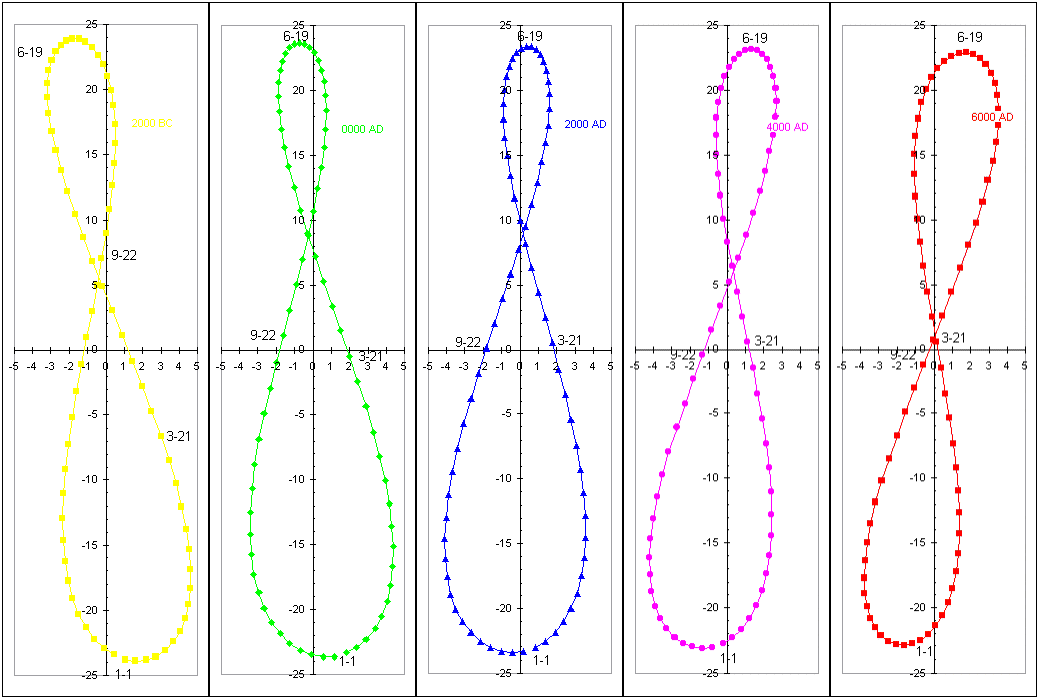
Two views of the variation of the Equation over Time. Graph by the Author, Analemmas by Pete Swanstrom
VARIATION OVER VERY LONG PERIODS
Video from Werner. Riegler showing the extreme changes to the EoT over very long periods. The main oscillation is the movement of the perihelion around the ecliptic, with a period of about 21000 years (which is a superposition of the platonic year - 25800 years -) and the perihelion motion - 110000 years).The difference in shape comes from eccentricity changes. The change due to obliquity is minor. The data used to generate this movie came from earth orbital parameters taken from NASA.
LAST SYMMETRICAL ANALEMMA
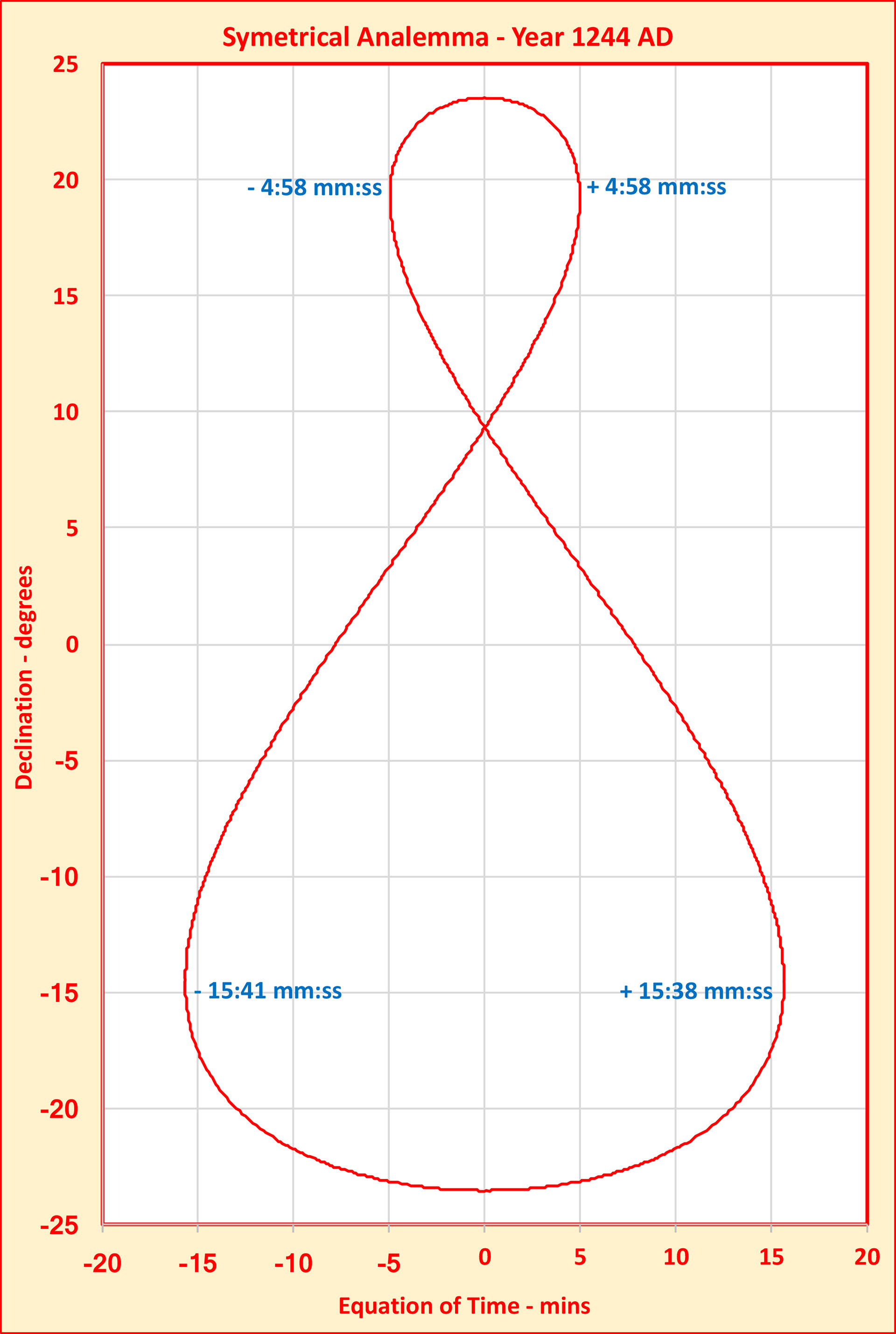
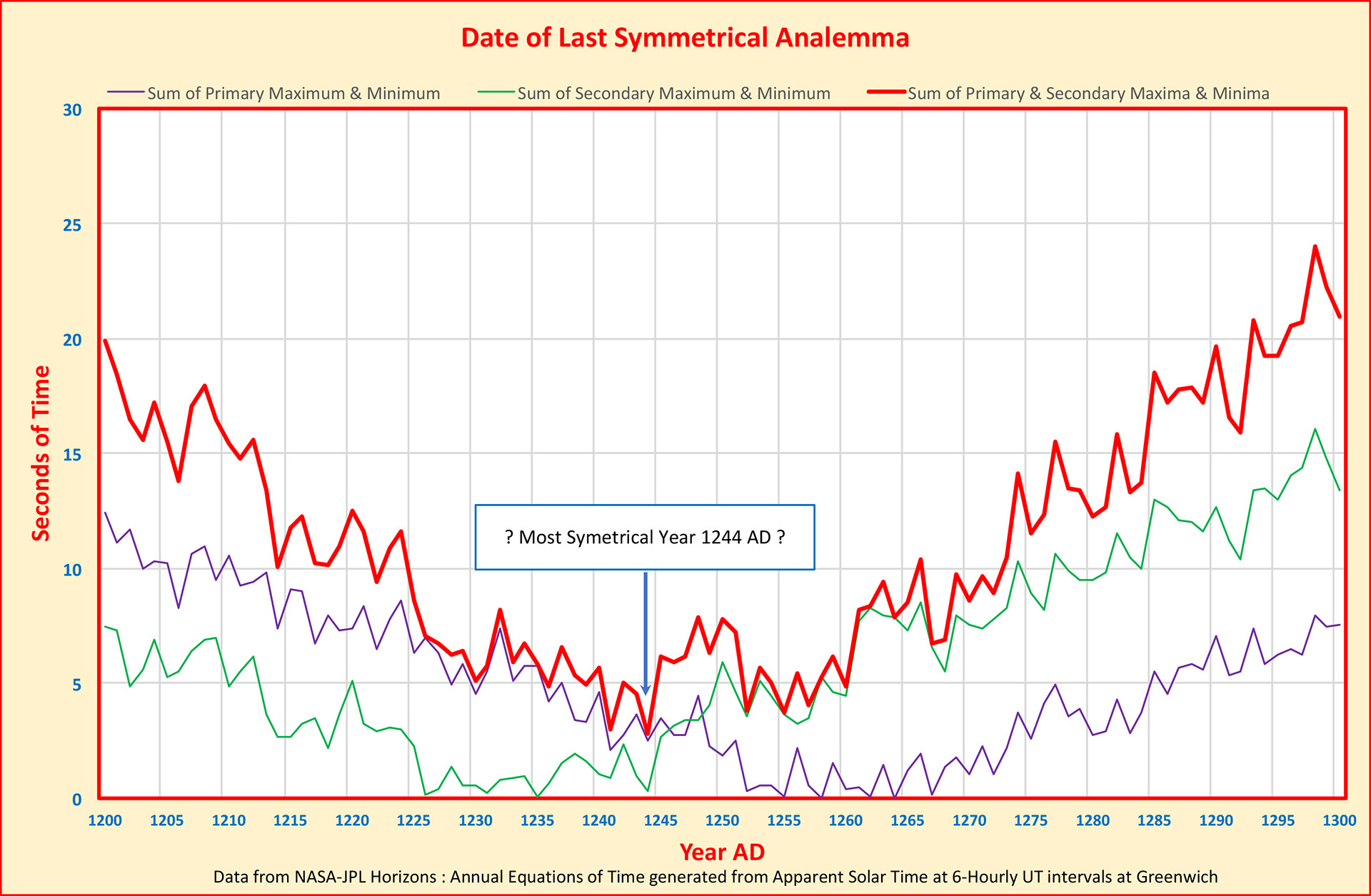
Since the shape of the Analemma is continuously varying, it is possible to find years in which the analemma is symmetrical. This is approximately when perihelion coincides with the solstices. Jan Meeus in his book "Astronomical Algorithms" found the year when this last took place to be 1246 CE. Another view of symmetry may be found by taking the sum of the maxima and minima of the EoT and find when this sum is minimum. The above graph suggests that the 1244 CE might claim that title! (Graphs by the author)